הפונקציה נקראת עולה על המרווח
, אם לנקודות כלשהן

את אי השוויון
(ערך גדול יותרהארגומנט מתאים לערך הגדול יותר של הפונקציה).

כמו כן, הפונקציה
שקוראים לו ירידה במרווח
, אם לנקודות כלשהן
מהמרווח הזה בתנאי
את אי השוויון
(ערך גדול יותר של הארגומנט מתאים לערך קטן יותר של הפונקציה).

הגדלת המרווח
וירידה במרווח
פונקציות נקראות מונוטוני במרווח
.

הכרת הנגזרת של פונקציה הניתנת להבדלה מאפשרת לנו למצוא מרווחים של המונוטוניות שלה.

משפט (תנאי מספיק כדי שהפונקציה תגדל).
פונקציות
חיובי על המרווח
, ואז הפונקציה
גדל באופן מונוטוני במרווח זה.

משפט (תנאי מספיק כדי שפונקציה תרד).אם הנגזרת ניתנת להפרדה על המרווח
פונקציות
שלילי על המרווח
, ואז הפונקציה
יורד באופן מונוטוני במרווח זה.

חוש גיאומטרי מהמשפטים הללו הוא שבמרווחים של פונקציה יורדת, הפונקציות המשיקות לגרף נוצרות עם הציר
זוויות קהות, ובמרווחי עלייה - חדים (ראה איור 1).

משפט (תנאי הכרחי למונוטוניות של פונקציה).אם הפונקציה
ניתן להבדיל ו
(
) על המרווח
, אז הוא לא יורד (לא עולה) במרווח זה.

אלגוריתם למציאת מרווחים של מונוטוניות של פונקציה
:

דוגמא.מצא מרווחי מונוטוניות של פונקציה
.

נְקוּדָה שקוראים לו נקודת מקסימום של הפונקציה

כזה עבור כולם , עומד בתנאי
, אי השוויון
.

תפקוד מקסימלי הוא הערך של הפונקציה בנקודת המקסימום.

איור 2 מציג דוגמה של גרף של פונקציה שיש לה מקסימום בנקודות
.

נְקוּדָה שקוראים לו נקודת מינימום של הפונקציה
אם יש מספר כלשהו
כזה עבור כולם , עומד בתנאי
, אי השוויון
. תאנה. לפונקציה 2 יש מינימום בנקודה .

יש שם נפוץ לשיאים ולנמוכים - קיצוניות . בהתאם, נקראות נקודות המקסימום והמינימום נקודות קיצון .

פונקציה המוגדרת על קטע יכולה לקבל מקסימום ומינימום רק בנקודות בתוך קטע זה. אי אפשר גם לבלבל בין המקסימום והמינימום של פונקציה לבין הערך המקסימלי והמינימלי שלה על פלח - אלו מושגים שונים מהותית.

בנקודות קיצון, לנגזרת תכונות מיוחדות.

משפט (תנאי הכרחי לקיצון).תן לנקודה פוּנקצִיָה
יש קיצון. אז גם
לא קיים, או
.

הנקודות האלה מהתחום של הפונקציה, שבהן
לא קיים או שבו
, נקראים נקודות קריטיות של הפונקציה .

לפיכך, נקודות הקיצון נמצאות בין הנקודות הקריטיות. במקרה הכללי, הנקודה הקריטית לא חייבת להיות נקודת קיצון. אם הנגזרת של פונקציה בנקודה מסוימת שווה לאפס, אין זה אומר שלפונקציה יש נקודת קיצון בנקודה זו.

דוגמא.לשקול
. יש לנו
, אבל נקודה
אינו נקודת קיצון (ראה איור 3).

משפט (התנאי הראשון המספיק לקיצוניות).תן לנקודה פוּנקצִיָה
מתמשך, והנגזרת
כאשר עוברים דרך נקודה משנה סימן. לאחר מכן – נקודת קיצון: מקסימום, אם הסימן משתנה מ-"+" ל-"–", ומינימום, אם מ-"-" ל-"+".

אם, כאשר עוברים דרך נקודה הנגזרת לא משנה סימן, אז בנקודה אין קיצון.

משפט (התנאי השני המספיק לקיצוניות).תן לנקודה נגזרת של פונקציה שניתנת להבדלה
שווה לאפס (
), והנגזרת השנייה שלו בשלב זה היא לא אפס (
) והוא רציף בחלק מהשכונה של הנקודה . לאחר מכן - נקודת קיצון
; בְּ-
היא נקודת המינימום, ו
זו נקודת המקסימום.

אלגוריתם למציאת נקודות קיצון של פונקציה תוך שימוש בתנאי הקיצון הראשון מספיק:

מצא נגזרת.

מצא נקודות קריטיות של הפונקציה.

בחן את הסימן של הנגזרת משמאל וימין של כל נקודה קריטית והסיק מסקנה לגבי נוכחות קיצוניות.

מצא את הערכים הקיצוניים של הפונקציה.

אלגוריתם למציאת נקודות קיצון של פונקציה באמצעות תנאי הקיצון השני מספיק:

דוגמא.מצא קיצוניות של פונקציה
.

עלייה, ירידה וקיצוניות של פונקציה

מציאת מרווחים של עלייה, ירידה וקיצוניות של פונקציה היא כמו משימה עצמאית, והחלק החשוב ביותר של משימות אחרות, בפרט, לימוד תפקוד מלא. מידע ראשוניעל הגידול, הירידה והקיצוניות של הפונקציה ניתנים ב פרק תיאורטי על הנגזרת, שאני ממליץ בחום למחקר מקדים (או חזרה)- גם מהסיבה שהחומר הבא מבוסס על העצם מהות הנגזרתלהיות המשך הרמוני של מאמר זה. אמנם, אם הזמן אוזל, אז אפשר גם עיבוד פורמלי גרידא של דוגמאות של השיעור של היום.

והיום יש רוח של תמימות דעים נדירה באוויר, ואני מרגיש ישירות שכל הנוכחים בוערים מרוב תשוקה למד לחקור פונקציה באמצעות נגזרת. לכן, מינוח נצחי סביר וטוב מופיע מיד על המסכים של המסכים שלך.

בשביל מה? אחת הסיבות המעשיות ביותר היא: כדי להבהיר מה בדרך כלל נדרש ממך במשימה מסוימת!

מונוטוניות פונקציה. נקודות קיצון ותפקוד אקסטרים

בואו נשקול פונקציה כלשהי. באופן פשטני, אנו מניחים זאת רָצִיףעל כל שורת המספרים:

ליתר ביטחון, מיד נפטר מאשליות אפשריות, במיוחד עבור אותם קוראים שהתוודעו לאחרונה מרווחים של קביעות הסימנים של הפונקציה. עכשיו אנחנו לא מעוניין, כיצד ממוקם הגרף של הפונקציה ביחס לציר (מעל, למטה, היכן שהוא חוצה את הציר). כדי לשכנע, מחק נפשית את הצירים והשאיר גרף אחד. כי העניין הוא בזה.

פוּנקצִיָה עולהעל מרווח אם עבור כל שתי נקודות של מרווח זה הקשורות ליחס , אי השוויון נכון. כלומר, ערך גדול יותר של הארגומנט מתאים לערך גדול יותר של הפונקציה, והגרף שלה עובר "מלמטה למעלה". פונקציית ההדגמה גדלה לאורך המרווח.

כמו כן, הפונקציה פּוֹחֵתעל מרווח אם עבור כל שתי נקודות של המרווח הנתון, כך , אי השוויון נכון. כלומר, ערך גדול יותר של הארגומנט מתאים לערך קטן יותר של הפונקציה, והגרף שלה הולך "מלמעלה למטה". הפונקציה שלנו פוחתת עם המרווחים .

אם פונקציה גדלה או יורדת על פני מרווח, אז היא נקראת מונוטוני למהדריןבמרווח זה. מהי מונוטוניות? קח את זה מילולית - מונוטוניות.

אפשר גם להגדיר לא יורדפונקציה (מצב רגוע בהגדרה הראשונה) ו לא מתגברפונקציה (מצב מרוכך בהגדרה השנייה). פונקציה לא יורדת או לא גדלה במרווח נקראת פונקציה מונוטונית במרווח נתון (מונוטוניות קפדנית היא מקרה מיוחד של מונוטוניות "סתם").

התיאוריה בוחנת גם גישות אחרות לקביעת עלייה/ירידה של פונקציה, כולל על חצאי מרווחים, מקטעים, אבל כדי לא לשפוך שמן-שמן-שמן על הראש שלך, אנו מסכימים לפעול במרווחים פתוחים עם הגדרות קטגוריות - זה ברור יותר, ולפתרון בעיות מעשיות רבות מספיק.

בדרך זו, במאמרים שלי, הניסוח "מונוטוניות של פונקציה" כמעט תמיד יסתתר מרווחיםמונוטוניות קפדנית(הגדלה קפדנית או ירידה קפדנית של הפונקציה).

שכונת נקודה. מילים שלאחריהן מתפזרים התלמידים לכל מקום שהם יכולים, ומתחבאים באימה בפינות. ...אם כי אחרי הפוסט גבולות קוצנייםהם כנראה לא מתחבאים יותר, אלא רק רועדים מעט =) אל תדאג, עכשיו לא יהיו הוכחות למשפטים של ניתוח מתמטי - הייתי צריך שהשכונה תנסח הגדרות בצורה קפדנית יותר נקודות קיצון. אנחנו זוכרים:

נקודת שכונהשם את המרווח שמכיל את הנקודה הנתונה, בעוד שלצורך נוחות מניחים כי המרווח הוא סימטרי. לדוגמה, נקודה והשכונה הסטנדרטית שלה:

בעיקרון ההגדרות:

הנקודה נקראת נקודת מקסימום קפדנית, אם קייםהשכונה שלה, לכולםערכים שפרט לנקודה עצמה, אי השוויון מתגשם. בשלנו דוגמה ספציפיתזו נקודה.

הנקודה נקראת נקודת מינימום קפדנית, אם קייםהשכונה שלה, לכולםערכים שפרט לנקודה עצמה, אי השוויון מתגשם. בשרטוט - נקודה "א".

הערה : הדרישה שהשכונה תהיה סימטרית אינה הכרחית כלל. בנוסף, זה חשוב עצם הקיוםשכונה (אם כי זעירה, אפילו מיקרוסקופית) שעונה על התנאים שצוינו

נקודות נקראות נקודות קיצון קפדניותאו בפשטות נקודות קיצוןפונקציות. כלומר, זהו מונח כללי למקסימום נקודות ומינימום נקודות.

איך להבין את המילה "קיצוני"? כן, בדיוק כמו מונוטוניות. נקודות קיצון של רכבת ההרים.

כמו במקרה של מונוטוניות, בתיאוריה קיימות ואף יותר נפוצות הנחות לא קפדניות (שתחתיו, כמובן, נופלים המקרים הנוקשים הנחשבים!):

הנקודה נקראת נקודת מקסימום, אם קייםסביבתו, כזו לכולם
הנקודה נקראת נקודת מינימום, אם קייםסביבתו, כזו לכולםהערכים של השכונה הזו, אי השוויון מתקיים.

שימו לב שלפי שתי ההגדרות האחרונות, כל נקודה של פונקציה קבועה (או "שטח שטוח" של פונקציה כלשהי) נחשבת גם לנקודת מקסימום וגם לנקודת מינימום! הפונקציה, אגב, היא גם לא גדלה וגם לא יורדת, כלומר מונוטונית. עם זאת, אנו משאירים את הטיעונים הללו לתיאורטיקנים, שכן בפועל אנו רואים כמעט תמיד את ה"גבעות" וה"שקעים" המסורתיים (ראו שרטוט) עם "מלך הגבעה" או "נסיכת הביצות" ייחודית. כמגוון, זה מתרחש נְקוּדָה, מכוון למעלה או למטה, למשל, המינימום של הפונקציה בנקודה .

אה, דרך אגב, הו תמלוגים:
- נקראת המשמעות מַקסִימוּםפונקציות;
- נקראת המשמעות מִינִימוּםפונקציות.

שם נפוץ - קיצוניותפונקציות.

אנא היזהר בדבריך!

נקודות קיצוןהם ערכי "x".
קיצוניות- ערכי "משחק".

! הערה : לפעמים המונחים הרשומים מתייחסים לנקודות "x-y" שנמצאות ישירות על ה-GRAPH של הפונקציה.

כמה אקסטרים יכולה להיות לפונקציה?

אין, 1, 2, 3 וכו'. עד אינסוף. לדוגמה, לסינוס יש מספר אינסופי של מינימום ומקסימום.

חָשׁוּב!המונח "פונקציה מקסימלית" לא מזוההמונח "ערך מקסימלי של פונקציה". קל לראות שהערך הוא מקסימום רק בשכונה המקומית, ויש "חברים יותר בפתאומיות" בשמאל העליון. כמו כן, "פונקציה מינימלית" אינה זהה ל"ערך פונקציה מינימלית", ובציור נוכל לראות שהערך הוא מינימום רק באזור מסוים. בהקשר זה, נקודות קיצון נקראות גם נקודות קיצון מקומיות, והאקסטרים קיצוניות מקומית. הם הולכים ומסתובבים ו גלוֹבָּלִיאַחִים לְדָת. אז לכל פרבולה יש בקודקוד שלה מינימום גלובליאוֹ מקסימום גלובלי. יתרה מכך, לא אבחין בין סוגי קיצון, וההסבר מושמע יותר למטרות חינוכיות כלליות - אין להפתיע את שמות התואר הנוספים "מקומי" / "עולמי".

בואו נסכם את הסטייה הקצרה שלנו אל התיאוריה עם זריקת בקרה: מה מרמזת המשימה "למצוא מרווחים של מונוטוניות ונקודות קיצון של פונקציה"?

הניסוח מבקש למצוא:

- מרווחים של עלייה / ירידה של התפקוד (לא יורדים, לא גדלים מופיעים הרבה פחות לעתים קרובות);

– נקודות מקסימום ו/או נקודות מינימום (אם יש). ובכן, עדיף למצוא את המינימום / המקסימום עצמם מהכישלון ;-)

איך להגדיר את כל זה?בעזרת פונקציה נגזרת!

איך למצוא מרווחים של עלייה, ירידה,
נקודות קיצון ונקודות קיצון של הפונקציה?

כללים רבים, למעשה, כבר ידועים ומובנים מהם שיעור על משמעות הנגזרת.

נגזרת טנגנטית נושא את החדשות הטובות שהפונקציה גדלה לאורך כל הדרך תחומים.

עם קוטנגנט ונגזרת שלו המצב הוא בדיוק הפוך.

הארקסין גדל על המרווח - הנגזרת חיובית כאן: .
עבור , הפונקציה מוגדרת אך לא ניתנת להבדלה. עם זאת, בנקודה הקריטית יש נגזרת יד ימין ומשיק יד ימין, ובקצה השני, מקביליהם משמאל.

אני חושב שלא יהיה לך קשה לבצע נימוקים דומים עבור arc cosinus ונגזרת שלו.

כל המקרים הללו, רבים מהם נגזרות טבלאיות, אני מזכיר לך, עקוב ישירות מ הגדרות של הנגזרת.

למה לחקור פונקציה עם נגזרת?

כדי לקבל מושג טוב יותר איך נראה הגרף של פונקציה זו: איפה זה הולך "מלמטה למעלה", איפה זה הולך "מלמעלה למטה", איפה זה מגיע לשפל של השיאים (אם בכלל). לא כל הפונקציות כל כך פשוטות - ברוב המקרים, בדרך כלל אין לנו שמץ של מושג לגבי הגרף של פונקציה מסוימת.

הגיע הזמן לעבור לדוגמאות משמעותיות יותר ולשקול אלגוריתם למציאת מרווחים של מונוטוניות וקיצוניות של פונקציה:

דוגמה 1

מצא מרווחים גדלים/קטנים וקיצוניות של פונקציה

פִּתָרוֹן:

1) הצעד הראשון הוא למצוא היקף פונקציה, וגם שימו לב לנקודות השבירה (אם הן קיימות). במקרה זה, הפונקציה רציפה על כל הקו האמיתי, והפעולה הזו היא רשמית במקצת. אבל במקרים מסוימים מתלקחות כאן יצרים רציניים, אז בואו נטפל בפסקה בלי להזניח.

2) הנקודה השנייה של האלגוריתם היא בשל

תנאי הכרחי לקיצוניות:

אם יש נקודת קיצון בנקודה, אז או שהערך לא קיים.

מבולבלים מהסוף? קיצוני של הפונקציה "מודולו x" .

תנאי הכרחי, אבל לא מספיק, וההיפך לא תמיד נכון. לכן, עדיין לא נובע מהשוויון שהפונקציה מגיעה למקסימום או למינימום בנקודה . דוגמה קלאסית כבר הודלקה למעלה - זו פרבולה מעוקבת והנקודה הקריטית שלה.

אבל כך או כך, תנאי הכרחיאקסטרום מכתיב את הצורך למצוא נקודות חשודות. כדי לעשות זאת, מצא את הנגזרת ופתור את המשוואה:

בתחילת המאמר הראשון לגבי גרפי פונקציותאמרתי לך איך לבנות פרבולה במהירות באמצעות דוגמה : "... אנו לוקחים את הנגזרת הראשונה ומשווים אותה לאפס: ... אז, הפתרון למשוואה שלנו: - זה בנקודה זו שממוקם החלק העליון של הפרבולה ...". עכשיו, אני חושב שכולם מבינים למה החלק העליון של הפרבולה נמצא בדיוק בנקודה הזו =) באופן כללי, כדאי להתחיל עם דוגמה דומה כאן, אבל היא פשוטה מדי (אפילו לקומקום). בנוסף, יש אנלוגי ממש בסוף השיעור על פונקציית נגזרת. אז בואו נעלה את הרמה:

דוגמה 2

מצא מרווחי מונוטוניות וקיצוניות של פונקציה

זו דוגמה של עשה זאת בעצמך. פתרון מלא ודגימת גמר משוערת של הבעיה בסוף השיעור.

הרגע המיוחל של הפגישה עם פונקציות רציונליות חלקיות הגיע:

דוגמה 3

חקור פונקציה באמצעות הנגזרת הראשונה

שימו לב כיצד ניתן לנסח מחדש את אותה משימה.

פִּתָרוֹן:

1) הפונקציה סובלת מהפסקות אינסופיות בנקודות.

2) אנו מזהים נקודות קריטיות. בוא נמצא את הנגזרת הראשונה ונשווה אותה לאפס:

בואו נפתור את המשוואה. שבר הוא אפס כאשר המונה שלו הוא אפס:

לפיכך, אנו מקבלים שלוש נקודות קריטיות:

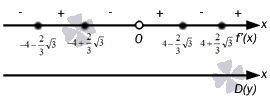
3) הנח בצד את כל הנקודות שזוהו על קו המספרים ו שיטת מרווחיםהגדירו את הסימנים של הנגזרת:

אני מזכיר לך שאתה צריך לקחת נקודה כלשהי מהמרווח, לחשב את הערך של הנגזרת שבו ולקבוע את הסימן שלו. יותר משתלם אפילו לא לספור, אלא "להעריך" מילולית. קח, למשל, נקודה השייכת למרווח , ובצע את ההחלפה: .

שני "פלוסים" ו"מינוס" אחד נותנים "מינוס", לכן, כלומר הנגזרת שלילית על כל המרווח.

הפעולה, כפי שאתה מבין, חייבת להתבצע עבור כל אחד מששת המרווחים. אגב, שימו לב שגורם המונה והמכנה חיוביים בהחלט עבור כל נקודה בכל מרווח, מה שמפשט מאוד את המשימה.

אז, הנגזרת אמרה לנו שהפונקציה עצמה גדלה ב- ויורד ב . נוח להדק מרווחים מאותו סוג עם סמל האיחוד.

בנקודה שהפונקציה מגיעה למקסימום שלה:
בנקודה שבה הפונקציה מגיעה למינימום שלה:

תחשוב למה אתה לא יכול לחשב מחדש את הערך השני ;-)

כשעוברים דרך נקודה, הנגזרת לא משנה סימן, ולכן לפונקציה אין שם קיצון - היא גם ירדה וגם נשארה יורדת.

! בואו נחזור נקודה חשובה : נקודות אינן נחשבות קריטיות - יש להן פונקציה לא מוגדר. בהתאם, כאן קיצוניות לא יכולות להיות עקרוניות(גם אם הנגזרת משנה סימן).

תשובה: הפונקציה גדלה ב- ויורד בנקודה שמגיעים למקסימום של הפונקציה: , ובנקודה - המינימום:.

ידע במרווחי מונוטוניות ואקסטרים, יחד עם מבוסס אסימפטוטיםנותן מושג טוב מאוד על מראה חיצוניגרף פונקציות. אדם ממוצע מסוגל לקבוע מילולית שלגרף של פונקציה יש שתי אסימפטוטות אנכיות ואסימפטוטה אלכסונית. הנה הגיבור שלנו:

נסה שוב לתאם את תוצאות המחקר עם הגרף של פונקציה זו.
אין קיצון בנקודה הקריטית, אבל יש הטיית עקומה(מה שקורה, ככלל, במקרים דומים).

דוגמה 4

מצא קיצוניות של פונקציה

דוגמה 5

מצא מרווחי מונוטוניות, מקסימום ומינימום של פונקציה

... סתם סוג של חג X-in-a-cube מסתבר היום ....
וואו, מי שם בגלריה הציע לשתות בשביל זה? =)

לכל משימה יש ניואנסים מהותיים ודקויות טכניות משלה, אשר מוזכרים בסוף השיעור.

כדי לקבוע את אופי הפונקציה ולדבר על התנהגותה, יש צורך למצוא מרווחים של עלייה וירידה. תהליך זה נקרא חקר פונקציות ותכנון. נקודת הקיצון משמשת כשמוצאים את הערכים הגדולים והקטנים ביותר של הפונקציה, מכיוון שהם מגדילים או מקטינים את הפונקציה מהמרווח.

מאמר זה חושף את ההגדרות, אנו מנסחים סימן מספיק לעלייה וירידה על המרווח והתנאי לקיומו של קיצון. זה חל על פתרון דוגמאות ובעיות. יש לחזור על הסעיף על בידול של פונקציות, כי בעת הפתרון יהיה צורך להשתמש במציאת הנגזרת.

Yandex.RTB R-A-339285-1 הגדרה 1

הפונקציה y = f (x) תגדל במרווח x כאשר עבור כל x 1 ∈ X ו- x 2 ∈ X , x 2 > x 1 אי השוויון f (x 2) > f (x 1) יהיה אפשרי. במילים אחרות, ערך גדול יותר של הארגומנט מתאים לערך גדול יותר של הפונקציה.

הגדרה 2

הפונקציה y = f (x) נחשבת יורדת במרווח x כאשר עבור כל x 1 ∈ X , x 2 ∈ X , x 2 > x 1 נחשב השוויון f (x 2) > f (x 1) אפשרי. במילים אחרות, ערך פונקציה גדול יותר מתאים לערך ארגומנט קטן יותר. שקול את האיור שלהלן.

תגובה: כאשר הפונקציה מוגדרת ורציפה בקצוות המרווח העולה והיורד, כלומר (א; ב) כאשר x = a, x = b, הנקודות נכללות במרווח העולה והיורד. זה לא סותר את ההגדרה, כלומר זה מתרחש במרווח x.

המאפיינים העיקריים של פונקציות אלמנטריות מהסוג y = sin x הם הגדרה והמשכיות עבור ערכים אמיתיים של הטיעונים. מכאן נקבל שהעלייה בסינוס מתרחשת על המרווח - π 2; π 2, אז לעלייה על הקטע יש את הצורה - π 2; π 2.

הגדרה 3

הנקודה x 0 נקראת נקודת מקסימוםעבור פונקציה y = f (x) כאשר עבור כל הערכים של x אי השוויון f (x 0) ≥ f (x) נכון. תפקוד מקסימליהוא הערך של הפונקציה בנקודה, והוא מסומן ב-y m a x .

הנקודה x 0 נקראת נקודת המינימום עבור הפונקציה y \u003d f (x) כאשר עבור כל הערכים של x אי השוויון f (x 0) ≤ f (x) נכון. מינימום תכונההוא ערך הפונקציה בנקודה, ובעל סימון הצורה y m i n.

השכונות של הנקודה x 0 נחשבות נקודות קיצון,וערך הפונקציה התואמת לנקודות הקיצון. שקול את האיור למטה.

אקסטרמה של הפונקציה עם הערך הגדול והקטן ביותר של הפונקציה. שקול את האיור למטה.

הדמות הראשונה אומרת שיש צורך למצוא את הערך הגדול ביותר של הפונקציה מהקטע [ a ; ב] . הוא נמצא באמצעות נקודות מקסימום ושווה לערך המקסימלי של הפונקציה, והנתון השני דומה יותר למציאת נקודת מקסימום ב-x = b.

תנאים מספיקים להגדלת והקטנת פונקציות

כדי למצוא את המקסימום והמינימום של פונקציה, יש צורך ליישם את הסימנים של קיצון במקרה שבו הפונקציה עומדת בתנאים אלה. התכונה הראשונה היא הנפוצה ביותר.

התנאי הראשון המספיק לקיצוניות

הגדרה 4

תינתן פונקציה y = f (x), הניתנת להבדלה בשכונת ε של הנקודה x 0 , ויש לה המשכיות בנקודה הנתונה x 0 . מכאן שאנחנו מקבלים את זה

• כאשר f "(x) > 0 עם x ∈ (x 0 - ε; x 0) ו-f" (x)< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• כאשר f"(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >0 עבור x ∈ (x 0 ; x 0 + ε), ואז x 0 היא נקודת המינימום.

במילים אחרות, אנו מקבלים את תנאי הגדרת השלטים שלהם:

• כאשר הפונקציה רציפה בנקודה x 0, אז יש לה נגזרת עם סימן משתנה, כלומר מ-+ ל-, כלומר הנקודה נקראת מקסימום;
• כאשר הפונקציה רציפה בנקודה x 0, אז יש לה נגזרת עם סימן משתנה מ- ל-+, כלומר הנקודה נקראת מינימום.

כדי לקבוע נכון את נקודות המקסימום והמינימום של הפונקציה, עליך לעקוב אחר האלגוריתם למציאתן:

• למצוא את תחום ההגדרה;
• למצוא את הנגזרת של הפונקציה באזור זה;
• לזהות אפסים ונקודות שבהן הפונקציה אינה קיימת;
• קביעת סימן הנגזרת על מרווחים;
• בחר את הנקודות שבהן הפונקציה משנה סימן.

שקול את האלגוריתם בדוגמה של פתרון מספר דוגמאות למציאת הקיצוניות של הפונקציה.

דוגמה 1

מצא את נקודות המקסימום והמינימום של הפונקציה הנתונה y = 2 (x + 1) 2 x - 2.

פִּתָרוֹן

התחום של פונקציה זו הוא כל המספרים הממשיים מלבד x = 2. ראשית, נמצא את הנגזרת של הפונקציה ונקבל:

y "= 2 x + 1 2 x - 2" = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2) " (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2) ) - (x + 2) 2 (x - 2) 2 = = 2 (x + 1) (x - 5) (x - 2) 2

מכאן אנו רואים שהאפסים של הפונקציה הם x \u003d - 1, x \u003d 5, x \u003d 2, כלומר יש להשוות כל סוגר לאפס. סמן על שורת המספרים וקבל:

כעת אנו קובעים את הסימנים של הנגזרת מכל מרווח. יש צורך לבחור נקודה הכלולה במרווח, להחליף אותה בביטוי. לדוגמה, נקודות x = - 2, x = 0, x = 3, x = 6.

אנחנו מקבלים את זה

y "(- 2) \u003d 2 (x + 1) (x - 5) (x - 2) 2 x \u003d - 2 \u003d 2 (- 2 + 1) (- 2 - 5) (- 2 - 2 ) 2 \u003d 2 7 16 \u003d 7 8 > 0, לפיכך, למרווח - ∞; - 1 יש נגזרת חיובית. באופן דומה, אנו מקבלים את זה

y "(0) = 2 (0 + 1) 0 - 5 0 - 2 2 = 2 - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

מאז המרווח השני התברר פחות מאפס, כך שהנגזרת על הקטע תהיה שלילית. השלישי עם מינוס, הרביעי עם פלוס. כדי לקבוע המשכיות, יש לשים לב לסימן של הנגזרת, אם הוא משתנה, אז זו נקודת קיצון.

נקבל שבנקודה x = - 1 הפונקציה תהיה רציפה, כלומר הנגזרת תשנה את הסימן מ-+ ל-. לפי הסימן הראשון, יש לנו ש-x = - 1 היא הנקודה המקסימלית, כלומר אנחנו מקבלים

y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0

הנקודה x = 5 מציינת שהפונקציה רציפה, והנגזרת תשנה את הסימן מ- ל-+. לפיכך, x=-1 היא נקודת המינימום, והממצא שלה הוא בעל הצורה

y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24

תמונה גרפית

תשובה: y m a x = y (- 1) = 0 , y m i n = y (5) = 24 .

כדאי לשים לב לעובדה שהשימוש בסימן מספיק ראשון של קיצון אינו מחייב את הפונקציה להיות ניתנת להבדלה מהנקודה x 0, וזה מפשט את החישוב.

דוגמה 2

מצא את נקודות המקסימום והמינימום של הפונקציה y = 1 6 x 3 = 2 x 2 + 22 3 x - 8.

פִּתָרוֹן.

התחום של פונקציה הוא כולו מספרים ממשיים. ניתן לכתוב זאת כמערכת של משוואות בצורה:

1 6 x 3 - 2 x 2 - 22 3 x - 8 , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

אז אתה צריך למצוא את הנגזרת:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 אינץ', x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

לנקודה x = 0 אין נגזרת, כי הערכים של הגבולות החד-צדדיים שונים. אנחנו מקבלים את זה:

lim y "x → 0 - 0 = lim yx → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 lim y "x → 0 + 0 = lim yx → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3

מכאן נובע שהפונקציה רציפה בנקודה x = 0, ואז אנו מחשבים

lim yx → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 (0 - 0) 3 - 2 (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 lim yx → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 ( 0 + 0) 2 + 22 3 (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 0 3 - 2 0 2 + 22 3 0 - 8 = - 8

יש צורך לבצע חישובים כדי למצוא את הערך של הארגומנט כאשר הנגזרת הופכת לאפס:

1 2 x 2 - 4 x - 22 3 , x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0

יש לסמן את כל הנקודות שהושגו על הקו כדי לקבוע את הסימן של כל מרווח. לכן, יש צורך לחשב את הנגזרת בנקודות שרירותיות עבור כל מרווח. לדוגמה, אנו יכולים לקחת נקודות עם ערכים x = -6, x = -4, x = -1, x = 1, x = 4, x = 6. אנחנו מקבלים את זה

y " (- 6) \u003d - 1 2 x 2 - 4 x - 22 3 x \u003d - 6 \u003d - 1 2 - 6 2 - 4 (- 6) - 22 3 \u003d - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y "(- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 (- 1) 2 - 4 (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

לתמונה על קו ישר יש את הצורה

אז, הגענו לנקודה שיש צורך לפנות לסימן הראשון של קיצון. אנחנו מחשבים ומקבלים את זה

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , מכאן לנקודות המקסימליות יש את הערכים x = - 4 + 2 3 3 , x = 4 - 2 3 3

נעבור לחישוב המינימום:

ymin = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 ymin = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 ymin = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

הבה נחשב את המקסימום של הפונקציה. אנחנו מקבלים את זה

ymax = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 ymax = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

תמונה גרפית

תשובה:

ymin = y - 4 - 2 3 3 = - 8 27 3 ymin = y (0) = - 8 ymin = y 4 + 2 3 3 = - 8 27 3 ymax = y - 4 + 2 3 3 = 8 27 3 ymax = y 4 - 2 3 3 = 8 27 3

אם ניתנת הפונקציה f "(x 0) = 0, אז עם f "" (x 0) > 0 נקבל ש-x 0 היא נקודת המינימום אם f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

דוגמה 3

מצא את המקסימום והמינימום של הפונקציה y = 8 x x + 1.

פִּתָרוֹן

ראשית, נמצא את תחום ההגדרה. אנחנו מקבלים את זה

D (y) : x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

יש צורך להבדיל את הפונקציה, ולאחר מכן אנו מקבלים

y "= 8 xx + 1" = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x

כאשר x = 1, הנגזרת הופכת להיות שווה לאפס, כלומר הנקודה היא נקודת קיצון אפשרית. לשם הבהרה, יש צורך למצוא את הנגזרת השנייה ולחשב את הערך ב-x \u003d 1. אנחנו מקבלים:

y "" = 4 - x + 1 (x + 1) 2 x " = = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x "(x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2" x + (x + 1) 2 x "(x + 1) 4 x == 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1)" x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1 ) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 - 4 8 = - 1< 0

לפיכך, באמצעות התנאי המספיק 2 עבור הקיצון, נקבל ש-x = 1 היא הנקודה המקסימלית. אחרת, הערך הוא y m a x = y (1) = 8 1 1 + 1 = 4 .

תמונה גרפית

תשובה: y m a x = y (1) = 4 ..

הגדרה 5

לפונקציה y = f (x) יש את הנגזרת שלה עד הסדר ה-n בשכונת ε של הנקודה הנתונה x 0 והנגזרת שלה עד הסדר n + 1 בנקודה x 0 . ואז f "(x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0 .

מכאן נובע שכאשר n הוא מספר זוגי, אז x 0 נחשבת לנקודת פיתול, כאשר n הוא מספר אי זוגי, אז x 0 היא נקודת קיצון, ו- f (n + 1) (x 0) > 0, ואז x 0 היא נקודת מינימום, f(n+1)(x0)< 0 , тогда x 0 является точкой максимума.

דוגמה 4

מצא את נקודות המקסימום והמינימום של הפונקציה y y = 1 16 (x + 1) 3 (x - 3) 4 .

פִּתָרוֹן

הפונקציה המקורית היא פונקציה רציונלית שלמה, ומכאן נובע שתחום ההגדרה הוא כל המספרים הממשיים. צריך להבדיל בין הפונקציה. אנחנו מקבלים את זה

y "= 1 16 x + 1 3" (x - 3) 4 + (x + 1) 3 x - 3 4 " == 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

נגזרת זו תלך לאפס ב-x 1 = - 1, x 2 = 5 7, x 3 = 3. כלומר, הנקודות יכולות להיות נקודות של קיצון אפשרי. יש צורך ליישם את תנאי הקיצון השלישי מספיק. מציאת הנגזרת השנייה מאפשרת לקבוע במדויק את הנוכחות של מקסימום ומינימום של פונקציה. הנגזרת השנייה מחושבת בנקודות הקיצון האפשרי שלה. אנחנו מקבלים את זה

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

זה אומר ש-x 2 \u003d 5 7 היא הנקודה המקסימלית. בהחלת 3 קריטריונים מספיקים, נקבל את זה עבור n = 1 ו-f (n + 1) 5 7< 0 .

יש צורך לקבוע את אופי הנקודות x 1 = - 1, x 3 = 3. כדי לעשות זאת, אתה צריך למצוא את הנגזרת השלישית, לחשב את הערכים בנקודות אלה. אנחנו מקבלים את זה

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " == 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

לפיכך, x 1 = - 1 היא נקודת הפיתול של הפונקציה, שכן עבור n = 2 ו- f (n + 1) (- 1) ≠ 0. יש צורך לחקור את הנקודה x 3 = 3. לשם כך, אנו מוצאים את הנגזרת הרביעית ומבצעים חישובים בשלב זה:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " == 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0

מהאמור לעיל, אנו מסיקים ש-x 3 \u003d 3 היא נקודת המינימום של הפונקציה.

תמונה גרפית

תשובה: x 2 \u003d 5 7 היא הנקודה המקסימלית, x 3 \u003d 3 - הנקודה המינימלית של הפונקציה הנתונה.

אם אתה מבחין בטעות בטקסט, אנא סמן אותה והקש Ctrl+Enter

"תפקוד מגדיל ומקטין"

מטרות השיעור:

1. למד למצוא מרווחים של מונוטוניות.

2. פיתוח יכולות מנטליות המספקות ניתוח המצב ופיתוח שיטות פעולה נאותות (ניתוח, סינתזה, השוואה).

3. יצירת עניין בנושא.

במהלך השיעורים

היום אנו ממשיכים ללמוד את היישום של הנגזרת ולשקול את שאלת היישום שלה לחקר פונקציות. עבודה קדמית

ועכשיו בואו ניתן כמה הגדרות למאפיינים של הפונקציה "סיעור מוחות".

1. מה נקרא פונקציה?

2. מה שמו של המשתנה x?

3. מה שמו של המשתנה Y?

4. מה ההיקף של פונקציה?

5. מהו קבוצת ערכי פונקציה?

6. מהי פונקציה זוגית?

7. איזו פונקציה נקראת אי זוגי?

8. מה ניתן לומר על הגרף של פונקציה זוגית?

9. מה ניתן לומר על הגרף של פונקציה אי זוגית?

10. מהי פונקציה מתגברת?

11. מהי פונקציה יורדת?

12. מהי פונקציה תקופתית?

מתמטיקה לומדת מודלים מתמטיים. אחד החשובים מודלים מתמטייםהיא פונקציה. קיים דרכים שונותתיאורי פונקציות. איזה מהם הכי ברור?

- גרפי.

- איך בונים גרף?

- לפי נקודות.

שיטה זו מתאימה אם יודעים מראש איך נראה הגרף. לדוגמה, מהו הגרף של פונקציה ריבועית, פונקציה לינארית, מידתיות הפוכה, פונקציה y = sinx? (הנוסחאות המתאימות מודגמות, התלמידים שמות את העקומות שהן גרפים.)

אבל מה אם אתה רוצה לצייר גרף של פונקציה או אפילו מורכבת יותר? אתה יכול למצוא מספר נקודות, אבל איך הפונקציה מתנהגת בין הנקודות הללו?

שים שתי נקודות על הלוח, בקשו מהתלמידים להראות איך הגרף "ביניהם" עשוי להיראות:

כדי לגלות כיצד פונקציה מתנהגת, הנגזרת שלה עוזרת.

פתחו מחברות, רשמו את המספר, עבודה בכיתה.

מטרת השיעור: למד כיצד גרף של פונקציה קשור לגרף של הנגזרת שלה, ולמד כיצד לפתור בעיות משני סוגים:

1. לפי הגרף של הנגזרת, מצא את מרווחי העלייה והירידה של הפונקציה עצמה, וכן את נקודות הקיצון של הפונקציה;

2. לפי סכימת הסימנים של הנגזרת על המרווחים, מצא את מרווחי העלייה והירידה של הפונקציה עצמה, כמו גם את נקודות הקיצון של הפונקציה.

משימות כאלה אינן בספרי הלימוד שלנו, אבל הן נמצאות במבחנים של הבחינה של המדינה המאוחדת (חלקים א' ו-ב').

היום בשיעור נשקול מרכיב קטן מהעבודה של השלב השני של לימוד התהליך, חקר אחד ממאפייני הפונקציה - קביעת מרווחים של מונוטוניות

כדי לפתור בעיה זו, עלינו להיזכר בכמה מהנושאים שנדונו קודם לכן.

אז, בואו נרשום את נושא השיעור של היום: סימנים של עלייה וירידה בפונקציות.

סימנים של עלייה וירידה בתפקוד:

אם הנגזרת של פונקציה זו חיובית עבור כל הערכים של x במרווח (a; c), כלומר f "(x)\u003e 0, אז הפונקציה גדלה במרווח זה.
אם הנגזרת של פונקציה זו שלילית עבור כל הערכים של x במרווח (a; b), כלומר f "(x)< 0, то функция в этом интервале убывает

סדר מציאת מרווחים של מונוטוניות:

מצא את היקף הפונקציה.

1. מצא את הנגזרת הראשונה של פונקציה.

2. להחליט על הלוח

מצא נקודות קריטיות, חקור את הסימן של הנגזרת הראשונה במרווחים שאליהם הנקודות הקריטיות שנמצאו מחלקות את תחום הפונקציה. מצא מרווחים של מונוטוניות של פונקציות:

א) תחום ההגדרה,

ב) מצא את הנגזרת הראשונה:,

ג) מצא את הנקודות הקריטיות: ; , ו

3. אנו חוקרים את הסימן של הנגזרת במרווחים המתקבלים, הפתרון מוצג בצורה של טבלה.

להצביע על נקודות קיצון

בואו נסתכל על כמה דוגמאות לבחינת פונקציה להגדלה והקטנה.

תנאי מספיק לקיומו של מקסימום הוא שינוי סימן הנגזרת במעבר בנקודה הקריטית מ-"+" ל-"-", ולמינימום מ-"-" ל-"+". אם הנגזרת לא משנה סימן במעבר דרך הנקודה הקריטית, אזי אין קיצון בנקודה זו

1. מצא את D(f).

2. מצא את f "(x).

3. מצא נקודות נייחות, כלומר. נקודות שבהן f"(x) = 0 או f"(x) לא קיימות.
(הנגזרת היא 0 באפסים של המונה, הנגזרת לא קיימת באפסים של המכנה)

4. אתר את D(f) ואת הנקודות הללו על קו הקואורדינטות.

5. קבע את הסימנים של הנגזרת בכל אחד מהמרווחים

6. החל שלטים.

7. רשמו את התשובה.

איחוד חומר חדש.

התלמידים עובדים בזוגות וכותבים את הפתרונות שלהם במחברות.

א) y \u003d x³ - 6 x² + 9 x - 9;

ב) y \u003d 3 x² - 5x + 4.

שני אנשים עובדים ליד הלוח.

א) y \u003d 2 x³ - 3 x² - 36 x + 40

ב) y \u003d x4-2 x³

3.סיכום השיעור

שיעורי בית: מבחן (מובחן)

מוֹנוֹטוֹנִיוּת

מאוד רכוש חשובהפונקציה היא המונוטוניות שלו. הכרת תכונה זו של פונקציות מיוחדות שונות, ניתן לקבוע את התנהגותם של תהליכים פיזיים, כלכליים, חברתיים ועוד רבים אחרים.

נבדלים בין הסוגים הבאים של מונוטוניות של פונקציות:

1) פוּנקצִיָה עולה, אם על מרווח כלשהו, ​​אם עבור כל שתי נקודות ומרווח זה כך . הָהֵן. ערך גדול יותר של הארגומנט מתאים לערך גדול יותר של הפונקציה;

2) פוּנקצִיָה פּוֹחֵת, אם על מרווח כלשהו, ​​אם עבור כל שתי נקודות ומרווח זה כך . הָהֵן. ערך גדול יותר של הארגומנט מתאים לערך קטן יותר של הפונקציה;

3) פוּנקצִיָה לא יורד, אם על מרווח כלשהו, ​​אם עבור כל שתי נקודות ומרווח זה כך ש;

4) פוּנקצִיָה אינו עולה, אם על מרווח כלשהו, ​​אם עבור כל שתי נקודות ומרווח זה כך .

2. בשני המקרים הראשונים נעשה שימוש גם במונח "מונוטוניות קפדנית".

3. שני המקרים האחרונים הם ספציפיים ולרוב מצוינים כהרכב של מספר פונקציות.

4. בנפרד, נציין שיש להתייחס לעלייה והירידה בגרף הפונקציה בדיוק משמאל לימין ותו לא.

2. זוגי אי - זוגי.

הפונקציה נקראת אי זוגי, אם כאשר הסימן של הטיעון משתנה, הוא משנה את ערכו להיפך. הנוסחה לכך נראית כך . המשמעות היא שאחרי החלפת ערכי מינוס x לפונקציה במקום כל האיקסים, הפונקציה תשנה את הסימן שלה. הגרף של פונקציה כזו הוא סימטרי לגבי המקור.

דוגמאות לפונקציות אי-זוגיות הן וכו'.

לדוגמה, הגרף אכן סימטרי לגבי המקור:

הפונקציה נקראת אפילואם שינוי הסימן של הארגומנט אינו משנה את ערכו. הנוסחה לכך נראית כך. המשמעות היא שלאחר החלפת ערכי מינוס x לפונקציה במקום כל ה-x, הפונקציה לא תשתנה כתוצאה מכך. הגרף של פונקציה כזו הוא סימטרי על הציר.

דוגמאות לפונקציות זוגיות הן וכו'.

לדוגמה, בואו נראה את הסימטריה של הגרף על הציר:

אם פונקציה אינה שייכת לאף אחד מהסוגים שצוינו, היא נקראת לא זוגית ולא אי זוגית, או פוּנקצִיָה השקפה כללית . לפונקציות כאלה אין סימטריה.

פונקציה כזו, למשל, היא הפונקציה הליניארית שנחשבה לאחרונה עם גרף:

3. תכונה מיוחדת של פונקציות היא תְקוּפָתִיוּת.

העובדה היא שהפונקציות התקופתיות הנחשבות בתכנית הלימודים הסטנדרטית של בית הספר הן רק פונקציות טריגונומטריות. כבר דיברנו עליהם בפירוט בעת לימוד הנושא המתאים.

פונקציה תקופתיתהיא פונקציה שאינה משנה את ערכה כאשר מספר קבוע שאינו אפס מתווסף לארגומנט.

המספר המינימלי הזה נקרא תקופת פונקציהומסומנים באות.

הנוסחה לכך נראית כך:

בואו נסתכל על תכונה זו בדוגמה של גרף סינוס:

נזכיר שהתקופה של הפונקציות והינה , והתקופה של ו היא .

כפי שאנו כבר יודעים, יכולה להיות תקופה לא סטנדרטית לפונקציות טריגונומטריות עם ארגומנט מורכב. אלו הן פונקציות של הטופס:

יש להם אותה תקופה. ולגבי פונקציות:

יש להם אותה תקופה.

כפי שאתה יכול לראות, כדי לחשב תקופה חדשה, התקופה הסטנדרטית מחולקת פשוט לפי הגורם בטיעון. זה לא תלוי בשינויים אחרים של הפונקציה.

הַגבָּלָה.

פוּנקצִיָה y=f(x) נקרא מוגבל מלמטה בקבוצה X⊂D(f) אם קיים מספר a כזה שעבור כל xϵX אי השוויון f(x)< a.

פוּנקצִיָה y=f(x) נקרא מוגבל מלמעלה בקבוצה X⊂D(f) אם קיים מספר a כזה שלכל xϵX אי השוויון f(x)< a.

אם המרווח X אינו מצוין, אזי זה נחשב שהפונקציה מוגבלת על פני כל תחום ההגדרה. פונקציה מוגבלת גם למעלה וגם למטה נקראת מוגבלת.

קל לקרוא את המגבלה של הפונקציה מהגרף. אפשר לצייר איזה קו ישר y=a, ואם הפונקציה גבוהה מהקו הישר הזה, אז היא תחומה מלמטה.

אם מתחת, אז בהתאמה למעלה. להלן גרף של פונקציה בעלת גבול נמוך יותר. גרף של פונקציה מוגבלת, חבר'ה, נסו לצייר אותה בעצמכם.

נושא: תכונות של פונקציות: מרווחי עלייה וירידה; הגדול ביותר ו הערך הקטן ביותר; נקודות קיצון (מקסימום ומינימום מקומיים), קמורות פונקציה.

תקופות של עלייה וירידה.

על בסיס תנאים מספיקים (סימנים) לעלייה וירידה של התפקוד, מוצאים את מרווחי העלייה והירידה של התפקוד.

להלן הניסוחים של הסימנים של עלייה וירידה בפונקציות במרווח:

אם הנגזרת של הפונקציה y=f(x)חיובי לכל אחד איקסמאינטרוול איקס, אז הפונקציה גדלה ב- איקס;

אם הנגזרת של הפונקציה y=f(x)שלילי לכל איקסמאינטרוול איקס, ואז הפונקציה יורדת ב- איקס.

לפיכך, כדי לקבוע את מרווחי העלייה והירידה של פונקציה, יש צורך:

למצוא את היקף הפונקציה;

למצוא את הנגזרת של פונקציה;

לפתור אי שוויון ובתחום ההגדרה;