מודולוס הוא הערך המוחלט של הביטוי. לפחות איכשהו לייעד מודול, נהוג להשתמש בסוגריים ישרים. הערך המוקף בסוגריים זוגיים הוא הערך שנלקח מודולו. תהליך פתרון כל מודול מורכב מפתיחת אותן סוגריים ישירים, הנקראים בשפה המתמטית סוגריים מודולריים. חשיפתם מתרחשת על פי מספר מסוים של כללים. כמו כן, בסדר פתרון המודולים, יש גם קבוצות של ערכים של אותם ביטויים שהיו בסוגריים של מודול. ברוב המקרים, המודול מורחב בצורה כזו שהביטוי שהיה תת-מודול מקבל ערכים חיוביים ושליליים, כולל הערך אפס. אם אתה סוטה מ להגדיר מאפייניםמודול, ואז בתהליך מורכבות משוואות או אי-שוויון שונות מהביטוי המקורי, שאותן צריך לפתור. בואו להבין איך לפתור מודולים.

תהליך פתרון

הפתרון של המודול מתחיל בכתיבת המשוואה המקורית עם המודול. כדי לענות על השאלה איך לפתור משוואות עם מודולוס, אתה צריך לפתוח אותו לחלוטין. כדי לפתור משוואה כזו, המודול מורחב. יש לקחת בחשבון את כל הביטויים המודולריים. יש לקבוע באילו ערכים של הכמויות הלא ידועות הכלולות בהרכבו, הביטוי המודולרי בסוגריים נעלם. כדי לעשות זאת, מספיק להשוות את הביטוי בסוגריים מודולריים לאפס, ולאחר מכן לחשב את הפתרון של המשוואה המתקבלת. יש לרשום את הערכים שנמצאו. באותו אופן, אתה גם צריך לקבוע את הערך של כל המשתנים הלא ידועים עבור כל המודולים במשוואה זו. לאחר מכן, יש לעסוק בהגדרה ובשיקול של כל המקרים של קיומם של משתנים בביטויים כאשר הם שונים מהערך אפס. כדי לעשות זאת, עליך לרשום מערכת כלשהי של אי שוויון התואמת לכל המודולים באי השוויון המקורי. יש לערוך את אי השוויון כך שיכסו את כל הערכים הזמינים והאפשריים עבור המשתנה שנמצאים על קו המספרים. אז אתה צריך לצייר להדמיה את אותו קו מספר, שעליו לשים את כל הערכים שהושגו בעתיד.

כיום ניתן לעשות כמעט הכל באינטרנט. המודול אינו חריג לכללים. אתה יכול לפתור את זה באינטרנט באחד המשאבים המודרניים הרבים. כל אותם ערכים של המשתנה שנמצאים במודול האפס יהיו אילוץ מיוחד שישמש בתהליך הפתרון משוואה מודולרית. במשוואה המקורית, נדרש להרחיב את כל הסוגריים המודולריים הזמינים, תוך שינוי סימן הביטוי כך שהערכים של המשתנה הרצוי עולים בקנה אחד עם אותם ערכים הנראים על קו המספרים. יש לפתור את המשוואה המתקבלת. יש לבדוק את ערך המשתנה, שיתקבל במהלך פתרון המשוואה, מול ההגבלה שנקבעה על ידי המודול עצמו. אם הערך של המשתנה עומד במלואו בתנאי, אז הוא נכון. יש להשליך את כל השורשים שיתקבלו במהלך פתרון המשוואה, אך לא יתאימו לאילוצים.

אנחנו לא בוחרים במתמטיקההמקצוע שלה, והיא בוחרת בנו.

המתמטיקאי הרוסי יו.אי. מנין

משוואות מודולו

הבעיות הקשות ביותר לפתרון במתמטיקה בבית הספר הן משוואות המכילות משתנים תחת סימן המודול. כדי לפתור בהצלחה משוואות כאלה, יש צורך לדעת את ההגדרה והמאפיינים הבסיסיים של המודול. מטבע הדברים, התלמידים צריכים להיות בעלי הכישורים לפתור משוואות מסוג זה.

מושגים ומאפיינים בסיסיים

מודולוס (ערך מוחלט) של מספר ממשימסומן והוא מוגדר כדלקמן:

ל מאפיינים פשוטיםהמודול כולל את היחסים הבאים:

פתק, ששני המאפיינים האחרונים מתקיימים בכל דרגה זוגית.

כמו כן, אם , איפה , אז ו

מאפייני מודול מורכבים יותר, אשר ניתן להשתמש ביעילות בפתרון משוואות עם מודולים, מנוסחים באמצעות המשפטים הבאים:

משפט 1.לכל פונקציה אנליטיתו את אי השוויון

משפט 2.שוויון זהה לאי שוויון.

משפט 3.שוויון שווה ערך לאי השוויון.

שקול דוגמאות טיפוסיות לפתרון בעיות בנושא "משוואות, המכיל משתנים תחת סימן המודול.

פתרון משוואות עם מודולוס

השיטה הנפוצה ביותר במתמטיקה בבית הספר לפתרון משוואות עם מודולוס היא השיטה, מבוסס על הרחבת מודול. שיטה זו היא גנרית, עם זאת, במקרה הכללי, היישום שלה יכול להוביל לחישובים מסורבלים מאוד. בהקשר זה, התלמידים צריכים להיות מודעים גם לאחרים, יותר שיטות יעילותושיטות לפתרון משוואות כאלה. באופן מיוחד, צריך את הכישורים ליישם משפטים, ניתן במאמר זה.

דוגמה 1פתור את המשוואה. (אחד)

פִּתָרוֹן. משוואה (1) תיפתר בשיטה ה"קלאסית" - שיטת הרחבת המודול. לשם כך, נשבור את הציר המספרינקודות ו מרווחים ושקול שלושה מקרים.

1. אם , אז , , , ומשוואה (1) מקבלת את הצורה . זה נובע מכאן. עם זאת, כאן, אז הערך שנמצא אינו שורש המשוואה (1).

2. אם, ואז ממשוואה (1) נקבלאו .

מאז שורש המשוואה (1).

3. אם , ואז משוואה (1) מקבלת את הצורהאו . ציין זאת .

תשובה: , .

בעת פתרון המשוואות הבאות עם המודול, נשתמש באופן פעיל במאפיינים של המודולים על מנת להגביר את היעילות של פתרון משוואות כאלה.

דוגמה 2פתור את המשוואה.

פִּתָרוֹן.מאז ו אז זה נובע מהמשוואה. בעניין זה, , , והמשוואה הופכת. מכאן אנחנו מקבלים. אבל , כך שלמשוואה המקורית אין שורשים.

תשובה: אין שורשים.

דוגמה 3פתור את המשוואה.

פִּתָרוֹן.מאז . אם, אז, והמשוואה הופכת.

מכאן אנו מקבלים.

דוגמה 4פתור את המשוואה.

פִּתָרוֹן.הבה נכתוב מחדש את המשוואה בצורה שווה ערך. (2)

המשוואה המתקבלת שייכת למשוואות מהסוג .

אם ניקח בחשבון את משפט 2, אנו יכולים לקבוע שמשוואה (2) שווה ערך לאי השוויון. מכאן אנו מקבלים.

תשובה: .

דוגמה 5פתור את המשוואה.

פִּתָרוֹן. למשוואה זו יש את הצורה. בגלל זה, לפי משפט 3, כאן יש לנו את אי השוויוןאו .

דוגמה 6פתור את המשוואה.

פִּתָרוֹן.בוא נניח ש. כי , אז המשוואה הנתונה לובשת צורה של משוואה ריבועית, (3)

איפה . מאז למשוואה (3) יש שורש חיובי יחידואז . מכאן נקבל שני שורשים של המשוואה המקורית:ו.

דוגמה 7 פתור את המשוואה. (4)

פִּתָרוֹן. מאז המשוואהשווה לשילוב של שתי משוואות:ו, אז בעת פתרון משוואה (4) יש צורך לשקול שני מקרים.

1. אם , אז או .

מכאן אנו מקבלים , ו .

2. אם , אז או .

מאז .

תשובה: , , , .

דוגמה 8פתור את המשוואה . (5)

פִּתָרוֹן.מאז ו , אז . מכאן ומשווה (5) יוצא כי ו, דהיינו. כאן יש לנו מערכת משוואות

עם זאת, מערכת משוואות זו אינה עקבית.

תשובה: אין שורשים.

דוגמה 9 פתור את המשוואה. (6)

פִּתָרוֹן.אם אנו מייעדים ומתוך משוואה (6) נקבל

או . (7)

מכיוון שלמשוואה (7) יש את הצורה , משוואה זו שווה ערך לאי השוויון . מכאן אנו מקבלים. מאז , אז או .

תשובה: .

דוגמה 10פתור את המשוואה. (8)

פִּתָרוֹן.לפי משפט 1, אנחנו יכולים לכתוב

(9)

בהתחשב במשוואה (8), אנו מסיקים ששני אי השוויון (9) הופכים לשוויון, כלומר. יש מערכת משוואות

עם זאת, לפי משפט 3, מערכת המשוואות הנ"ל מקבילה למערכת אי השוויון

(10)

פתרון מערכת אי השוויון (10) נקבל . מכיוון שמערכת אי השוויון (10) שווה ערך למשוואה (8), למשוואה המקורית יש שורש בודד.

תשובה: .

דוגמה 11. פתור את המשוואה. (11)

פִּתָרוֹן.תן ו , אז המשוואה (11) מרמזת על השוויון .

מכאן נובע כי ו. לפיכך, כאן יש לנו מערכת של אי-שוויון

הפתרון למערכת אי השוויון הזו הםו.

תשובה: , .

דוגמה 12.פתור את המשוואה. (12)

פִּתָרוֹן. משוואה (12) תיפתר בשיטה של ​​הרחבה רצופה של מודולים. לשם כך, שקול מספר מקרים.

1. אם , אז .

1.1. אם , אז ו , .

1.2. אם, אז. אבל , לכן, במקרה זה, למשוואה (12) אין שורשים.

2. אם , אז .

2.1. אם , אז ו , .

2.2. אם , אז ו .

תשובה: , , , , .

דוגמה 13פתור את המשוואה. (13)

פִּתָרוֹן.מכיוון שהצד השמאלי של המשוואה (13) אינו שלילי, אז ו. בהקשר זה, ומשוואה (13)

לוקח את הטופס או .

ידוע כי המשוואה שווה לשילוב של שתי משוואותו, פתרון שאנו מקבלים, . כי , אז למשוואה (13) יש שורש אחד.

תשובה: .

דוגמה 14 פתור מערכת משוואות (14)

פִּתָרוֹן.מאז ו , אז ו . לכן, ממערכת המשוואות (14) נקבל ארבע מערכות משוואות:

השורשים של מערכות המשוואות הנ"ל הם השורשים של מערכת המשוואות (14).

תשובה: ,, , , , , , .

דוגמה 15 פתור מערכת משוואות (15)

פִּתָרוֹן.מאז . בהקשר זה, ממערכת המשוואות (15) אנו מקבלים שתי מערכות משוואות

השורשים של מערכת המשוואות הראשונה הם ו , וממערכת המשוואות השנייה נקבל ו .

תשובה: , , , .

דוגמה 16 פתור מערכת משוואות (16)

פִּתָרוֹן.מהמשוואה הראשונה של המערכת (16) עולה כי .

מאז . שקול את המשוואה השנייה של המערכת. ככל ש, לאחר מכן , והמשוואה הופכת, , או .

אם נחליף את הערךלתוך המשוואה הראשונה של המערכת (16), אז , או .

תשובה: , .

ללימוד מעמיק יותר של שיטות פתרון בעיות, קשור לפתרון משוואות, המכיל משתנים תחת סימן המודול, אתה יכול לייעץ להדרכות מרשימת הספרות המומלצת.

1. אוסף משימות במתמטיקה למועמדים לאוניברסיטאות טכניות / אד. מִי. סקנאווי. - מ.: עולם וחינוך, 2013. - 608 עמ'.

2. Suprun V.P. מתמטיקה לתלמידי תיכון: משימות מורכבות מוגברת. - מ .: KD "ליברוקום" / URSS, 2017. - 200 עמ'.

3. Suprun V.P. מתמטיקה לתלמידי תיכון: שיטות לא סטנדרטיות לפתרון בעיות. - מ .: KD "ליברוקום" / URSS, 2017. - 296 עמ'.

יש לך שאלות?

לקבלת עזרת מורה דרך - הירשמו.

אתר, עם העתקה מלאה או חלקית של החומר, נדרש קישור למקור.

אחד הנושאים הקשים ביותר לתלמידים הוא פתרון משוואות המכילות משתנה תחת סימן המודולוס. בואו נראה בתור התחלה למה זה קשור? מדוע, למשל, רוב הילדים לוחצים על משוואות ריבועיות כמו אגוזים, אבל עם כאלה מושג מורכבאיך למודול יש כל כך הרבה בעיות?

לדעתי, כל הקשיים הללו קשורים בהיעדר כללים מנוסחים בבירור לפתרון משוואות עם מודולוס. לכן, כאשר פותרים משוואה ריבועית, התלמיד יודע בוודאות שעליו ליישם תחילה את הנוסחה המבחנה, ולאחר מכן את הנוסחאות לשורשי המשוואה הריבועית. אבל מה אם נתקלים במודול במשוואה? ננסה לתאר בבירור את תוכנית הפעולה הדרושה למקרה כאשר המשוואה מכילה לא ידוע תחת סימן המודול. אנו נותנים מספר דוגמאות לכל מקרה.

אבל קודם כל, בואו נזכור הגדרת מודול. אז, המודולוס של המספר אהמספר עצמו נקרא if אלא שלילי ו -אאם המספר א פחות מאפס. אתה יכול לכתוב את זה כך:

|א| = a אם a ≥ 0 ו- |a| = -a אם א< 0

אם כבר מדברים על המשמעות הגיאומטרית של המודול, יש לזכור שכל מספר ממשי מתאים לנקודה מסוימת על ציר המספרים - שלו ל לְתַאֵם. אז, המודול או הערך המוחלט של מספר הוא המרחק מנקודה זו למקור הציר המספרי. המרחק ניתן תמיד כמספר חיובי. לפיכך, המודולוס של כל מספר שלילי הוא מספר חיובי. אגב, גם בשלב זה תלמידים רבים מתחילים להתבלבל. כל מספר יכול להיות במודול, אבל התוצאה של יישום המודול היא תמיד מספר חיובי.

כעת נעבור לפתרון המשוואות.

1. שקול משוואה בצורה |x| = c, כאשר c הוא מספר ממשי. ניתן לפתור משוואה זו באמצעות הגדרת המודולוס.

נחלק את כל המספרים הממשיים לשלוש קבוצות: אלה שגדולים מאפס, אלה שקטנים מאפס, והקבוצה השלישית היא המספר 0. נכתוב את הפתרון בצורה של דיאגרמה:

(±c אם c > 0

אם |x| = c, ואז x = (0 אם c = 0

(אין שורשים אם עם< 0

1) |x| = 5, כי 5 > 0, ואז x = ±5;

2) |x| = -5, כי -חָמֵשׁ< 0, то уравнение не имеет корней;

3) |x| = 0, ואז x = 0.

2. משוואה בצורה |f(x)| = b, כאשר b > 0. כדי לפתור משוואה זו, יש צורך להיפטר מהמודלוס. אנו עושים זאת כך: f(x) = b או f(x) = -b. כעת יש צורך לפתור בנפרד כל אחת מהמשוואות שהתקבלו. אם במשוואה המקורית ב< 0, решений не будет.

1) |x + 2| = 4, כי 4 > 0, אם כן

x + 2 = 4 או x + 2 = -4

2) |x 2 – 5| = 11, כי 11 > 0, אם כן

x 2 - 5 = 11 או x 2 - 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 ללא שורשים

3) |x 2 – 5x| = -8 , כי -8< 0, то уравнение не имеет корней.

3. משוואה בצורה |f(x)| = g(x). לפי משמעות המודול, למשוואה כזו יהיו פתרונות אם הצד הימני שלה גדול או שווה לאפס, כלומר. g(x) ≥ 0. אז יש לנו:

f(x) = g(x)אוֹ f(x) = -g(x).

1) |2x – 1| = 5x - 10. למשוואה זו יהיו שורשים אם 5x - 10 ≥ 0. כאן מתחיל הפתרון של משוואות כאלה.

1. או.ד.ז. 5x – 10 ≥ 0

2. פתרון:

2x - 1 = 5x - 10 או 2x - 1 = -(5x - 10)

3. שלבו O.D.Z. והפתרון, אנחנו מקבלים:

השורש x \u003d 11/7 לא מתאים לפי O.D.Z. הוא קטן מ-2, ו-x \u003d 3 עונה על תנאי זה.

תשובה: x = 3

2) |x – 1| \u003d 1 - x 2.

1. או.ד.ז. 1 - x 2 ≥ 0. בואו נפתור את אי השוויון הזה בשיטת המרווחים:

(1 – x)(1 + x) ≥ 0

2. פתרון:

x - 1 \u003d 1 - x 2 או x - 1 \u003d - (1 - x 2)

x 2 + x - 2 = 0 x 2 - x = 0

x = -2 או x = 1 x = 0 או x = 1

3. שלב פתרון ו-O.D.Z.:

רק השורשים x = 1 ו-x = 0 מתאימים.

תשובה: x = 0, x = 1.

4. משוואה בצורה |f(x)| = |g(x)|. משוואה כזו מקבילה לשתי המשוואות הבאות f(x) = g(x) או f(x) = -g(x).

1) |x 2 - 5x + 7| = |2x – 5|. משוואה זו מקבילה לשניים הבאים:

x 2 - 5x + 7 = 2x - 5 או x 2 - 5x +7 = -2x + 5

x 2 - 7x + 12 = 0 x 2 - 3x + 2 = 0

x = 3 או x = 4 x = 2 או x = 1

תשובה: x = 1, x = 2, x = 3, x = 4.

5. משוואות שנפתרו בשיטת ההחלפה (שינוי משתנה). השיטה הזאתהכי קל להסביר את הפתרונות דוגמה ספציפית. אז תינתן משוואה ריבועית עם מודולוס:

x 2 – 6|x| + 5 = 0. לפי המאפיין של המודול x 2 = |x| 2, כך שניתן לשכתב את המשוואה באופן הבא:

|x| 2–6|x| + 5 = 0. בוא נעשה את השינוי |x| = t ≥ 0, אז יהיה לנו:

t 2 - 6t + 5 \u003d 0. בפתרון המשוואה הזו, נקבל ש-t \u003d 1 או t \u003d 5. בוא נחזור להחלפה:

|x| = 1 או |x| = 5

x = ±1 x = ±5

תשובה: x = -5, x = -1, x = 1, x = 5.

בואו נסתכל על דוגמה נוספת:

x 2 + |x| – 2 = 0. לפי המאפיין של המודול x 2 = |x| 2, אז

|x| 2 + |x| – 2 = 0. בוא נעשה את השינוי |x| = t ≥ 0, ואז:

t 2 + t - 2 \u003d 0. כשפותרים את המשוואה הזו, נקבל, t \u003d -2 או t \u003d 1. בוא נחזור להחלפה:

|x| = -2 או |x| = 1

אין שורשים x = ± 1

תשובה: x = -1, x = 1.

6. סוג נוסף של משוואות הוא משוואות בעלות מודולוס "מורכב". משוואות כאלה כוללות משוואות שיש להן "מודולים בתוך מודול". ניתן לפתור משוואות מסוג זה באמצעות המאפיינים של המודול.

1) |3 – |x|| = 4. נפעל באותו אופן כמו במשוואות מהסוג השני. כי 4 > 0, אז נקבל שתי משוואות:

3 – |x| = 4 או 3 – |x| = -4.

כעת נבטא את המודול x בכל משוואה, ואז |x| = -1 או |x| = 7.

אנו פותרים כל אחת מהמשוואות שהתקבלו. אין שורשים במשוואה הראשונה, כי -אחד< 0, а во втором x = ±7.

תשובה x = -7, x = 7.

2) |3 + |x + 1|| = 5. אנו פותרים את המשוואה הזו בצורה דומה:

3 + |x + 1| = 5 או 3 + |x + 1| = -5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 או x + 1 = -2. אין שורשים.

תשובה: x = -3, x = 1.

קיימת גם שיטה אוניברסלית לפתרון משוואות עם מודולוס. זוהי שיטת הריווח. אבל נשקול זאת עוד יותר.

אתר, עם העתקה מלאה או חלקית של החומר, נדרש קישור למקור.

בית ספר תיכון MBOU №17 Ivanov

« משוואות מודולו»
פיתוח מתודי

מלוקט

מורה למתמטיקה

Lebedeva N.V.

20010

הערת הסבר

פרק 1 - מבוא

סעיף 2. מאפיינים עיקריים סעיף 3. פרשנות גיאומטרית למושג המודולוס של מספר סעיף 4. גרף הפונקציה y = |x| סעיף 5 אמנות

פרק 2

סעיף 1. משוואות בצורה |F(х)| = m (פרוטוזואה) סעיף 2. משוואות בצורה F(|х|) = m סעיף 3. משוואות בצורה |F(х)| = G(x) סעיף 4. משוואות בצורה |F(х)| = ± F(x) (יפה) סעיף 5. משוואות בצורה |F(х)| = |G(x)| סעיף 6. דוגמאות לפתרון משוואות לא סטנדרטיות סעיף 7. משוואות בצורה |F(х)| + |G(x)| = 0 סעיף 8. משוואות הצורה |а 1 x ± в 1 | ± |a 2 x ± ב-2 | ± …|a n x ± ב-n | = מ סעיף 9. משוואות המכילות מודולים מרובים

פרק 3. דוגמאות לפתרון משוואות שונות עם מודולוס.

סעיף 1. משוואות טריגונומטריות סעיף 2 משוואות אקספוננציאליות סעיף 3 משוואות לוגריתמיות סעיף 4. משוואות אי-רציונליות סעיף 5. משימות בעלות מורכבות מתקדמת תשובות לתרגילים בִּיבּלִיוֹגְרָפִיָה

הערת הסבר.

מושג הערך המוחלט (מודולוס) של מספר ממשי הוא אחד המאפיינים המהותיים שלו. מושג זה נמצא בשימוש נרחב בענפים שונים של מדעים פיזיקליים, מתמטיים וטכניים. בתרגול של הוראת קורס מתמטיקה בבית ספר תיכון בהתאם לתוכנית של משרד ההגנה של הפדרציה הרוסית, המושג "ערך מוחלט של מספר" נתקל שוב ושוב: בכיתה ו', ההגדרה של מודול , המשמעות הגאומטרית שלו, מוצגת; בכיתה ח' נוצר מושג הטעות המוחלטת, נבחן פתרון המשוואות והאי-שוויון הפשוטים ביותר המכילים את המודולוס, תכונות החשבון שורש ריבועי; בכיתה יא', המושג נמצא בסעיף "שורש נתואר".ניסיון ההוראה מראה שלעתים קרובות התלמידים נתקלים בקשיים בפתרון משימות הדורשות ידע בחומר זה, ולעיתים מדלגים לפני שמתחילים להשלים. בטקסטים של מטלות בחינה לקורס כיתות ט' ויא' נכללות גם משימות דומות. בנוסף, הדרישות שהאוניברסיטאות מטילות על בוגרי בתי הספר שונות, כלומר יותר רמה גבוההמהדרישות של תכנית הלימודים בבית הספר. לחיים ב חברה מודרניתחשוב מאוד הוא היווצרות של סגנון חשיבה מתמטי, המתבטא במיומנויות מנטליות מסוימות. בתהליך פתרון בעיות עם מודולים, נדרשת היכולת ליישם טכניקות כגון הכללה וקונקרטיזציה, ניתוח, סיווג וסיסטמטיזציה, אנלוגיה. הפתרון של משימות כאלה מאפשר לך לבדוק את הידע של החלקים העיקריים של הקורס בבית הספר, הרמה חשיבה לוגית, כישורי מחקר ראשוניים. העבודה הזומוקדש לאחד הסעיפים - פתרון המשוואות המכילות את המודול. הוא מורכב משלושה פרקים. הפרק הראשון מציג את מושגי היסוד ואת החישובים התיאורטיים החשובים ביותר. הפרק השני מציע תשעה סוגים בסיסיים של משוואות המכילות את המודול, בוחן שיטות לפתרונן ומנתח דוגמאות לרמות שונות של מורכבות. הפרק השלישי מציע משוואות מורכבות יותר ולא סטנדרטיות (טריגונומטריות, אקספוננציאליות, לוגריתמיות ואי-רציונליות). לכל סוג משוואות יש תרגילים לפתרון עצמאי (מצורפות תשובות והנחיות). המטרה העיקרית של עבודה זו היא מתן סיוע מתודולוגי למורים בהכנה לשיעורים ובארגון קורסי בחירה. החומר יכול לשמש גם כ מדריך לימודלתלמידי תיכון. המשימות המוצעות בעבודה מעניינות ולא תמיד קלות לפתרון, מה שמאפשר להפוך את מוטיבציית הלמידה של התלמידים למודעים יותר, לבחון את יכולותיהם ולשפר את רמת ההכנה של בוגרי בית הספר לכניסה לאוניברסיטאות. מבחר מובחן של התרגילים המוצעים מרמז על מעבר מרמת הרבייה של הטמעת החומר לזו היצירתית, כמו גם הזדמנות ללמד כיצד ליישם את הידע שלהם בפתרון בעיות לא סטנדרטיות.

פרק 1 - מבוא.

סעיף 1. קביעת הערך המוחלט .

הַגדָרָה : הערך המוחלט (מודולוס) של מספר ממשי אבלנקרא מספר לא שלילי: אבלאוֹ -אבל. יִעוּד: │ אבל │ הערך כתוב כך: "מודול של המספר a" או "ערך מוחלט של המספר a"

│ a if a > 0

│a│ = │ 0 אם a = 0 (1)

│ - א, אם א
דוגמאות: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

הרחב מודול ביטוי:

א) │x - 8│ אם x > 12 ב) │2x + 3│ אם x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

סעיף 2. מאפיינים בסיסיים.

שקול את המאפיינים הבסיסיים של הערך המוחלט. נכס מס' 1: למספרים מנוגדים יש מודולים שווים, כלומר. │а│=│-а│הבה נראה את נכונות השוויון. נרשום את ההגדרה של המספר - אבל : │- a│= (2) הבה נשווה בין קבוצות (1) ו-(2). ברור, ההגדרות של הערכים האבסולוטיים של המספרים אבלו - אבלהתאמה. כתוצאה מכך, │а│=│-а│
כאשר בוחנים את המאפיינים הבאים, אנו מגבילים את עצמנו לניסוח שלהם, מכיוון שההוכחה שלהם ניתנת נכס מס' 2: הערך המוחלט של הסכום של מספר סופי של מספרים ממשיים אינו עולה על סכום הערכים המוחלטים של המונחים: נכס מס' 3: הערך המוחלט של ההפרש בין שני מספרים ממשיים אינו חורג מסכום ערכם המוחלט: │а - │ ≤│а│+│в│ נכס מס' 4: הערך המוחלט של המכפלה של מספר סופי של מספרים ממשיים שווה למכפלת הערכים המוחלטים של הגורמים: │а · в│=│а│·│в│ נכס מס' 5: הערך המוחלט של המנה של המספרים הממשיים שווה למנה של הערכים המוחלטים שלהם:

סעיף 3. פרשנות גיאומטרית למושג המודולוס של מספר.

ניתן לשייך כל מספר ממשי לנקודה על קו המספרים, שתהווה ייצוג גיאומטרי של המספר האמיתי הזה. כל נקודה על קו המספרים מתאימה למרחק שלה מהמקור, כלומר. אורך הקטע מהמקור לנקודה הנתונה. מרחק זה נחשב תמיד כערך לא שלילי. לכן, אורך המקטע המתאים יהיה הפרשנות הגיאומטרית של הערך המוחלט של המספר הממשי הנתון

האיור הגיאומטרי המוצג מאשר בבירור נכס מס' 1, כלומר. מודולים של מספרים מנוגדים שווים. מכאן ניתן להבין בקלות את תקפות השוויון: │x - a│= │a - x│. זה גם הופך ברור יותר לפתור את המשוואה │х│= m, כאשר m ≥ 0, כלומר x 1.2 = ± m. דוגמאות: 1) │х│= 4 x 1.2 = ± 4 2) │х - 3│= 1
x 1.2 = 2; 4

סעיף 4. גרף של הפונקציה y \u003d │х│

התחום של פונקציה זו הוא כולו מספרים ממשיים.

סעיף 5. סמלים.

בעתיד, כאשר בוחנים דוגמאות לפתרון משוואות, ישמשו את הדברים הבאים. מוסכמות: ( - סימן מערכת [ - סימן קבע כאשר פותרים מערכת משוואות (אי-שוויון), נמצא המפגש בין פתרונות המשוואות (אי-שוויון) הכלולים במערכת. כאשר פותרים קבוצת משוואות (אי-שוויון), נמצא איחוד של פתרונות של המשוואות (אי-שוויון) הכלולים בקבוצה.

פרק 2

בפרק זה, נבחן דרכים אלגבריות לפתור משוואות המכילות מודול אחד או יותר.

סעיף 1. משוואות בצורה │F (х) │= m

משוואה מסוג זה נקראת הפשוטה ביותר. יש לה פתרון אם ורק אם m ≥ 0. לפי הגדרת המודולוס, המשוואה המקורית שווה ערך לשילוב של שתי משוואות: │ ו(x)│=M
דוגמאות:
№1. פתרו את המשוואה: │7x - 2│= 9


תשובה: x 1 = - 1; איקס 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 \u003d -2 x (x + 3) \u003d 0 x 1 \u003d 0; x 2 = -3 תשובה: סכום השורשים הוא - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 מציין x 2 = m, m ≥ 0 x = 0 ; ±√5 מ' 2 – 5 מ' + 4 = 0 מ' = 1; 4 - שני הערכים עומדים בתנאי m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 תשובה: מספר השורשים של משוואה 7. תרגילים:
№1. פתרו את המשוואה וציינו את סכום השורשים: │x - 5│= 3 №2 . פתרו את המשוואה וציינו את השורש הקטן יותר: │x 2 + x │ \u003d 0 №3 . פתרו את המשוואה וציינו את השורש הגדול יותר: │x 2 - 5x + 4 │ \u003d 4 №4 פתרו את המשוואה וציינו את כל השורש: │2x 2 - 7x + 6│ \u003d 1 №5 פתרו את המשוואה וציינו את מספר השורשים: │x 4 - 13x 2 + 50 │ = 14

סעיף 2. משוואות בצורה F(│х│) = m

ארגומנט הפונקציה בצד שמאל נמצא מתחת לסימן מודולו, בעוד שהצד הימני אינו תלוי במשתנה. הבה נבחן שתי דרכים לפתרון משוואות מסוג זה. דרך אחת:לפי הגדרת הערך המוחלט, המשוואה המקורית שווה ערך למכלול של שתי מערכות. בכל אחד מהם מוטל תנאי על הביטוי של תת-מודול. ו(│х│) =M
מכיוון שהפונקציה F(│х│) היא זוגית בכל תחום ההגדרה, שורשי המשוואות F(х) = m ו-F(-х) = m הם זוגות של מספרים מנוגדים. לכן, די לפתור את אחת המערכות (כאשר בוחנים את הדוגמאות בצורה זו, יינתן הפתרון של מערכת אחת). דו כיווני:יישום שיטת הכנסת משתנה חדש. במקרה זה, ייעוד │х│= a מוצג, כאשר a ≥ 0. השיטה הזאתפחות נפח בעיצוב.
דוגמאות: №1 . פתרו את המשוואה: 3x 2 - 4│x│ = - 1 בואו נשתמש בהקדמה של משתנה חדש. סמן │x│= a, כאשר a ≥ 0. נקבל את המשוואה 3a 2 - 4a + 1 = 0 D = 16 - 12 = 4 a 1 = 1 a 2 = 1 / 3 נחזור למשתנה המקורי: │x │ = 1 ו-│х│= 1/3. לכל משוואה שני שורשים. תשובה: x 1 = 1; איקס 2 = - 1; איקס 3 = 1 / 3 ; איקס 4 = - 1 / 3 . №2. פתרו את המשוואה: 5x 2 + 3│x│- 1 \u003d 1 / 2 │x│ + 3x 2
בוא נמצא את הפתרון של מערכת הסט הראשון: 4x 2 + 5x - 2 \u003d 0 D \u003d 57 x 1 \u003d -5 + √57 / 8 x 2 \u003d -5-√57 / 8 שימו לב ש-x 2 כן לא מקיים את התנאי x ≥ 0. לפי הפתרון המערכת השנייה תהיה המספר ההפוך x 1. תשובה: x 1 = -5+√57 / 8 ; איקס 2 = 5-√57 / 8 .№3 . פתור את המשוואה: x 4 - │х│= 0 סמן │х│= a, כאשר a ≥ 0. נקבל את המשוואה a 4 - a \u003d 0 a (a 3 - 1) \u003d 0 a 1 \u003d 0 a 2 \u003d 1 נחזור למשתנה המקורי: │х│=0 ו│х│= 1 x = 0; ± 1 תשובה: x 1 = 0; איקס 2 = 1; איקס 3 = - 1.
תרגילים: №6. פתרו את המשוואה: 2│х│ - 4.5 = 5 - 3/8 │х│ №7 . פתרו את המשוואה, בתשובה ציינו את מספר השורשים: 3x 2 - 7│x│ + 2 = 0 №8 . פתרו את המשוואה, בתשובה ציינו את כל הפתרונות: x 4 + │х│ - 2 = 0

סעיף 3. משוואות בצורה │F(х)│ = G(х)

הצד הימני של משוואה מסוג זה תלוי במשתנה ולכן יש לו פתרון אם ורק אם הצד הימני הוא פונקציה G(x) ≥ 0. ניתן לפתור את המשוואה המקורית בשתי דרכים: דרך אחת:תקן, המבוסס על גילוי המודול על בסיס הגדרתו ומורכב ממעבר שווה ערך לשילוב של שתי מערכות. │ ו(x)│ =G(איקס)

זה רציונלי להשתמש בשיטה זו במקרה של ביטוי מורכב עבור הפונקציה G(x) וביטוי מורכב פחות עבור הפונקציה F(x), שכן היא אמורה לפתור אי שוויון עם הפונקציה F(x). דו כיווני:הוא מורכב ממעבר למערכת מקבילה שבה מוטל תנאי בצד ימין. │ ו(איקס)│= G(איקס)

שיטה זו נוחה יותר לשימוש אם הביטוי עבור הפונקציה G(x) פחות מסובך מאשר עבור הפונקציה F(x), שכן מניחים את הפתרון של אי השוויון G(x) ≥ 0. בנוסף, במקרה מתוך מספר מודולים, שיטה זו מומלץ להשתמש באפשרות השנייה. דוגמאות: №1. פתרו את המשוואה: │x + 2│= 6 -2x
(דרך אחת) תשובה: x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(דו כיוונים) תשובה: מכפלת השורשים היא 3.
№3. פתרו את המשוואה, בתשובה רשמו את סכום השורשים:
│x - 6 │ \u003d x 2 - 5x + 9

תשובה: סכום השורשים הוא 4.
תרגילים: №9. │x + 4│= - 3x №10. פתרו את המשוואה, בתשובה ציינו את מספר הפתרונות: │x 2 + x - 1 │ \u003d 2x - 1 №11 . פתרו את המשוואה, בתשובה ציינו את מכפלת השורשים: │x + 3 │ \u003d x 2 + x - 6

סעיף 4. משוואות בצורה │F(x)│= F(x) ו│F(x)│= - F(x)

משוואות מסוג זה נקראות לפעמים "יפות". מכיוון שהצד הימני של המשוואות תלוי במשתנה, קיימים פתרונות אם ורק אם הצד הימני אינו שלילי. לכן, המשוואות המקוריות שוות לאי השוויון:
│F(x)│= F(x) F(x) ≥ 0 ו-│F(x)│= - F(x) F(x) דוגמאות: №1 . פתרו את המשוואה, בתשובה ציינו את השורש השלם הקטן יותר: │5x - 3│ \u003d 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0.6 תשובה: x = 1№2. פתרו את המשוואה, בתשובה ציינו את אורך הפער: │x 2 - 9 │ \u003d 9 - x 2 x 2 - 9 ≤ 0 (x - 3) (x + 3) ≤ 0 [- 3; 3] תשובה: אורך הפער הוא 6.№3 . פתרו את המשוואה, בתשובה ציינו את מספר פתרונות המספרים השלמים: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] תשובה: 4 פתרונות שלמים.№4 . פתרו את המשוואה, בתשובה ציינו את השורש הגדול ביותר:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 \u003d 0 D \u003d 5 x 1.2 \u003d
≈ 1,4

תשובה: x = 3.

תרגילים: №12. פתרו את המשוואה, בתשובה ציינו את כל השורש: │x 2 + 6x + 8 │= x 2 + 6x + 8 №13. פתרו את המשוואה, בתשובה ציינו את מספר פתרונות המספרים השלמים: │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. פתרו את המשוואה, בתשובה ציינו מספר שלם שאינו שורש המשוואה:

סעיף 5. משוואות בצורה │F(x)│= │G(x)│

מכיוון ששני הצדדים של המשוואה אינם שליליים, הפתרון כולל התייחסות לשני מקרים: ביטויי תת-מודולים שווים או מנוגדים בסימן. לכן, המשוואה המקורית שווה ערך לשילוב של שתי משוואות: │ ו(איקס)│= │ G(איקס)│
דוגמאות: №1. פתרו את המשוואה, בתשובה ציינו את כל השורש: │x + 3│ \u003d │2x - 1│
תשובה: שורש מספר שלם x = 4.№2. פתור את המשוואה: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
תשובה: x = 2.№3 . פתרו את המשוואה, בתשובה ציינו את מכפלת השורשים:




שורשי המשוואה 4x 2 + 2x - 1 \u003d 0 x 1.2 \u003d - 1±√5 / 4 תשובה: מכפלת השורשים היא 0.25. תרגילים: №15 . פתרו את המשוואה, בתשובה ציינו את כל הפתרון: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. פתרו את המשוואה, בתשובה ציינו את השורש הקטן יותר: │5x - 3│=│7 - x│ №17 . פתרו את המשוואה, בתשובה רשמו את סכום השורשים:

סעיף 6. דוגמאות לפתרון משוואות לא סטנדרטיות

בחלק זה נבחן דוגמאות של משוואות לא סטנדרטיות, שבפתרון שלהן מתגלה הערך המוחלט של הביטוי בהגדרה. דוגמאות:

№1. פתרו את המשוואה, בתשובה ציינו את סכום השורשים: x │x│- 5x - 6 \u003d 0
תשובה: סכום השורשים הוא 1 №2. . פתרו את המשוואה, בתשובה ציינו את השורש הקטן יותר: x 2 - 4x
- 5 = 0
תשובה: שורש קטן יותר x = -5. №3. פתור את המשוואה:

תשובה: x = -1. תרגילים: №18. פתרו את המשוואה וכתבו את סכום השורשים: x │3x + 5│= 3x 2 + 4x + 3
№19. פתרו את המשוואה: x 2 - 3x \u003d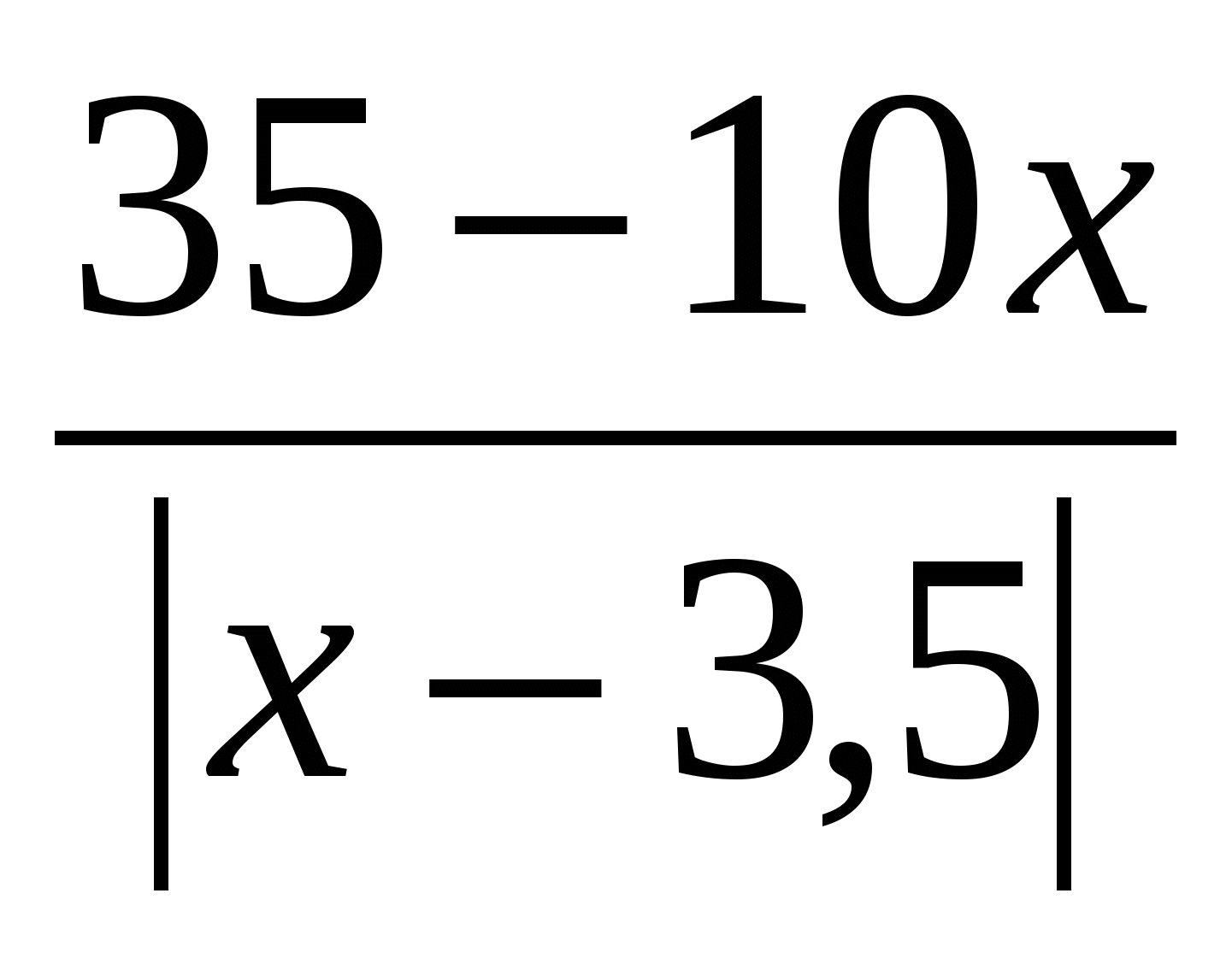

№20. פתור את המשוואה:

סעיף 7. משוואות בצורה │F(x)│+│G(x)│=0

קל לראות שבצד שמאל של משוואה מסוג זה, סכום הכמויות הלא שליליות. לכן, למשוואה המקורית יש פתרון אם ורק אם שני האיברים שווים לאפס בו זמנית. המשוואה מקבילה למערכת המשוואות: │ ו(איקס)│+│ G(איקס)│=0
דוגמאות: №1 . פתור את המשוואה:
תשובה: x = 2. №2. פתור את המשוואה: תשובה: x = 1. תרגילים: №21. פתור את המשוואה: №22 . פתרו את המשוואה, בתשובה רשמו את סכום השורשים: №23 . פתרו את המשוואה, בתשובה ציינו את מספר הפתרונות:

סעיף 8. משוואות הצורה

כדי לפתור משוואות מסוג זה, נעשה שימוש בשיטת המרווחים. אם זה נפתר על ידי הרחבה רציפה של מודולים, אז אנחנו מקבלים נסטים של מערכות, וזה מאוד מסורבל ולא נוח. שקול את האלגוריתם של שיטת המרווחים: 1). מצא ערכים משתנים איקס, שעבורו כל מודול שווה לאפס (אפסים של ביטויי תת-מודולים):
2). הערכים שנמצאו מסומנים על קו מספרים, המחולק למרווחים (מספר המרווחים, בהתאמה, שווה ל- נ+1 ) 3). קבע עם איזה סימן כל מודול מתגלה בכל אחד מהמרווחים שהתקבלו (בעת יצירת פתרון, ניתן להשתמש בקו מספר, לסמן עליו את הסימנים) 4). המשוואה המקורית שווה ערך לקבוצה נ+1 מערכות, שבכל אחת מהן מצוינת החברות במשתנה איקסאחד המרווחים. דוגמאות: №1 . פתרו את המשוואה, בתשובה ציינו את השורש הגדול ביותר:
אחד). בואו נמצא את האפסים של ביטויי תת-מודול: x = 2; x = -3 2). אנו מסמנים את הערכים שנמצאו על קו המספרים וקובעים באיזה סימן כל מודול מתגלה במרווחים שהתקבלו:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- אין פתרונות למשוואה יש שני שורשים. תשובה: השורש הגדול ביותר הוא x = 2. №2. פתרו את המשוואה, כתבו את כל השורש בתשובה:
אחד). בואו נמצא את האפסים של ביטויי תת-מודול: x = 1.5; x = - 1 2). אנו מסמנים את הערכים שנמצאו על קו המספרים וקובעים באיזה סימן כל מודול מתגלה במרווחים שהתקבלו: x + 1 x + 1 x + 1 - + +
-1 1.5 х 2х - 3 2х - 3 2х - 3 - - +
3).
למערכת האחרונה אין פתרונות, לכן, למשוואה יש שני שורשים. בעת פתרון המשוואה, עליך לשים לב לסימן "-" מול המודול השני. תשובה: שורש מספר שלם x = 7. №3. פתרו את המשוואה, בתשובה ציינו את סכום השורשים: 1). בואו נמצא את האפסים של ביטויי תת-מודול: x = 5; x = 1; x = - 2 2). אנו מסמנים את הערכים שנמצאו על קו המספרים וקובעים באיזה סימן כל מודול מתגלה במרווחים שהתקבלו: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
למשוואה יש שני שורשים x = 0 ו-2. תשובה: סכום השורשים הוא 2. №4 . פתרו את המשוואה: 1). בואו נמצא את האפסים של ביטויי תת-מודול: x = 1; x = 2; x = 3. 2). הבה נקבע את הסימן שבו כל מודול מורחב במרווחים שהושגו. 3).
אנו משלבים את הפתרונות של שלוש המערכות הראשונות. תשובה: ; x = 5.
תרגילים: №24. פתור את המשוואה:
№25. פתרו את המשוואה, בתשובה רשמו את סכום השורשים: №26. פתרו את המשוואה, בתשובה ציינו את השורש הקטן יותר: №27. פתרו את המשוואה, תן את השורש הגדול יותר בתשובתך:

סעיף 9. משוואות המכילות מודולים מרובים

משוואות המכילות מודולים מרובים מניחות נוכחות של ערכים מוחלטים בביטויי תת-מודולים. העיקרון הבסיסי של פתרון משוואות מסוג זה הוא חשיפה רציפה של מודולים, החל ב"חיצוני". במהלך הפתרון נעשה שימוש בטכניקות הנדונות בסעיפים מס' 1, מס' 3.

דוגמאות: №1. פתור את המשוואה:
תשובה: x = 1; - אחת עשרה. №2. פתור את המשוואה:
תשובה: x = 0; 4; - 4. №3. פתרו את המשוואה, בתשובה ציינו את מכפלת השורשים:
תשובה: מכפלת השורשים היא 8. №4. פתור את המשוואה:
סמן את משוואות האוכלוסיה (1) ו (2) ושקול את הפתרון של כל אחד מהם בנפרד לנוחות העיצוב. מכיוון ששתי המשוואות מכילות יותר ממודול אחד, נוח יותר לבצע מעבר שווה ערך לקבוצות של מערכות. (1)

(2)


תשובה:
תרגילים: №36. פתרו את המשוואה, בתשובה ציינו את סכום השורשים: 5 │3x-5│ \u003d 25 x №37. פתרו את המשוואה, אם יש יותר משורש אחד, בתשובה ציינו את סכום השורשים: │x + 2│ x - 3x - 10 = 1 №38. פתרו את המשוואה: 3 │2x -4│ \u003d 9 │x│ №39. פתרו את המשוואה, בתשובה ציינו את מספר השורשים עבור: 2 │ sin x │ = √2 №40 . פתרו את המשוואה, בתשובה ציינו את מספר השורשים:

סעיף 3. משוואות לוגריתמיות.

לפני פתרון המשוואות הבאות, יש צורך לסקור את תכונות הלוגריתמים ואת הפונקציה הלוגריתמית. דוגמאות: №1. פתרו את המשוואה, בתשובה ציינו את מכפלת השורשים: log 2 (x + 1) 2 + log 2 │x + 1 │ \u003d 6 O.D.Z. x+1≠0 x≠ - 1

מקרה 1: אם x ≥ - 1, אז log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – עומד בתנאי x ≥ - 1 2 מקרה: אם x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 לוג 2 (-(x+1) 3) = לוג 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – עומד בתנאי x - 1
תשובה: מכפלת השורשים היא 15.
№2. פתרו את המשוואה, בתשובה ציינו את סכום השורשים: lg
או.ד.ז.

תשובה: סכום השורשים הוא 0.5.
№3. פתרו את המשוואה: יומן 5
או.ד.ז.

תשובה: x = 9. №4. פתרו את המשוואה: │2 + log 0.2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 בואו נשתמש בנוסחה למעבר לבסיס אחר. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 בואו נמצא את האפסים של ביטויי תת-מודול: x = 25; x \u003d המספרים האלה מחלקים את שטח הערכים המותרים לשלושה מרווחים, כך שהמשוואה שווה ערך לסך של שלוש מערכות.
תשובה: )