Essential properties of a trapezoid. Material on geometry on the topic "trapezoid and its properties"

In order to feel confident and successfully solve problems in geometry lessons, it is not enough to learn formulas. They need to be understood first. To be afraid, and even more so to hate formulas, is unproductive. In this article, accessible language will be analyzed various ways finding the area of ​​a trapezoid. For a better assimilation of the corresponding rules and theorems, we will pay some attention to its properties. This will help you understand how the rules work and in what cases certain formulas should be applied.

Define a trapezoid

What is this figure in general? A trapezoid is a polygon with four angles and two parallel sides. The other two sides of the trapezoid can be tilted at different angles. Its parallel sides are called bases, and for non-parallel sides, the name "sides" or "hips" is used. Such figures are quite common in everyday life. The contours of the trapezoid can be seen in the silhouettes of clothing, interior items, furniture, dishes and many others. Trapeze happens different types: versatile, isosceles and rectangular. We will analyze their types and properties in more detail later in the article.

Trapezoid Properties

Let us dwell briefly on the properties of this figure. The sum of the angles adjacent to any side is always 180°. It should be noted that all the angles of a trapezoid add up to 360°. The trapezoid has the concept of a midline. If you connect the midpoints of the sides with a segment, this will be the middle line. It is designated m. The middle line has important properties: it is always parallel to the bases (we remember that the bases are also parallel to each other) and equal to their half-sum:

This definition must be learned and understood, because it is the key to solving many problems!

At the trapezoid, you can always lower the height to the base. An altitude is a perpendicular, often denoted by the symbol h, which is drawn from any point on one base to another base or its extension. The midline and height will help you find the area of ​​the trapezoid. Such tasks are the most common in the school geometry course and regularly appear among control and examination papers.

The simplest formulas for the area of ​​a trapezoid

Let's analyze the two most popular and simple formulas with which to find the area of ​​a trapezoid. It is enough to multiply the height by half the sum of the bases to easily find what you are looking for:

S = h*(a + b)/2.

In this formula, a, b denote the bases of the trapezoid, h - the height. For readability in this article, multiplication signs are marked with the symbol (*) in formulas, although in official reference books the multiplication sign is usually omitted.

Consider an example.

Given: a trapezoid with two bases equal to 10 and 14 cm, height is 7 cm. What is the area of ​​the trapezoid?

Let's analyze the solution to this problem. Using this formula, you first need to find the half-sum of the bases: (10 + 14) / 2 \u003d 12. So, the half-sum is 12 cm. Now we multiply the half-sum by the height: 12 * 7 \u003d 84. The desired is found. Answer: The area of ​​a trapezoid is 84 square meters. cm.

The second well-known formula says: the area of ​​a trapezoid is equal to the product of the midline and the height of the trapezoid. That is, it actually follows from the previous concept of the middle line: S=m*h.

Using Diagonals for Calculations

Another way to find the area of ​​a trapezoid is actually not that hard. It is connected with its diagonals. According to this formula, to find the area, it is required to multiply the half-product of its diagonals (d 1 d 2) by the sine of the angle between them:

S = ½ d 1 d 2 sin a.

Consider a problem that shows the application of this method. Given: a trapezoid with a diagonal length of 8 and 13 cm, respectively. The angle a between the diagonals is 30°. Find the area of ​​the trapezoid.

Decision. Using the above formula, it is easy to calculate what is required. As you know, sin 30 ° is 0.5. Therefore, S = 8*13*0.5=52. Answer: The area is 52 square meters. cm.

Looking for the area of ​​an isosceles trapezoid

A trapezoid can be isosceles (isosceles). Its sides are the same And the angles at the bases are equal, which is well illustrated in the figure. An isosceles trapezoid has the same properties as a regular trapezoid, plus a number of special ones. A circle can be circumscribed around an isosceles trapezoid, and a circle can be inscribed in it.

What are the methods for calculating the area of ​​\u200b\u200bsuch a figure? The method below will require a lot of calculations. To use it, you need to know the values ​​​​of the sine (sin) and cosine (cos) of the angle at the base of the trapezoid. Their calculations require either Bradis tables or an engineering calculator. Here is the formula:

S= c*sin a*(a - c* cos a),

where with- lateral thigh a- angle at the lower base.

An isosceles trapezoid has diagonals of the same length. The converse is also true: if the diagonals of a trapezoid are equal, then it is isosceles. Hence the following formula to help find the area of ​​a trapezoid - the half-product of the square of the diagonals and the sine of the angle between them: S = ½ d 2 sin a.

Finding the area of ​​a rectangular trapezoid

A special case of a rectangular trapezoid is known. This is a trapezoid, in which one side (her thigh) adjoins the bases at a right angle. It has the properties of an ordinary trapezoid. In addition, she has a very interesting feature. The difference of the squares of the diagonals of such a trapezoid is equal to the difference of the squares of its bases. For it, all the previously given methods for calculating the area are used.

Applying ingenuity

There is one trick that can help in case of forgetfulness of specific formulas. Let's take a closer look at what a trapezoid is. If we mentally divide it into parts, then we will get familiar and understandable geometric shapes: a square or a rectangle and a triangle (one or two). If you know the height and sides of the trapezoid, you can use the formulas for the area of ​​\u200b\u200ba triangle and rectangle, and then add up all the obtained values.

Let's illustrate this with the following example. Given a rectangular trapezoid. Angle C = 45°, angles A, D are 90°. The upper base of the trapezoid is 20 cm, the height is 16 cm. It is required to calculate the area of ​​\u200b\u200bthe figure.

This figure obviously consists of a rectangle (if two angles are 90°) and a triangle. Since the trapezoid is rectangular, therefore, its height is equal to its side, that is, 16 cm. We have a rectangle with sides of 20 and 16 cm, respectively. Consider now a triangle whose angle is 45°. We know that one side of it is 16 cm. Since this side is also the height of the trapezoid (and we know that the height falls on the base at a right angle), therefore, the second angle of the triangle is 90 °. Hence the remaining angle of the triangle is 45°. As a consequence of this, we get a right-angled isosceles triangle, in which two sides are the same. This means that the other side of the triangle is equal to the height, that is, 16 cm. It remains to calculate the area of ​​\u200b\u200bthe triangle and the rectangle and add the resulting values.

The area of ​​a right triangle is equal to half the product of its legs: S = (16*16)/2 = 128. The area of ​​a rectangle is equal to the product of its width and length: S = 20*16 = 320. We found the required one: the area of ​​the trapezoid S = 128 + 320 = 448 sq. see. You can easily double-check yourself using the above formulas, the answer will be identical.

We use the Pick formula

Finally, we present one more original formula that helps to find the area of ​​a trapezoid. It's called the Pick formula. It is convenient to use it when the trapezoid is drawn on checkered paper. Similar tasks are often found in the materials of the GIA. It looks like this:

S \u003d M / 2 + N - 1,

in this formula, M is the number of nodes, i.e. intersections of the lines of the figure with the lines of the cell on the borders of the trapezoid (orange dots in the figure), N is the number of nodes inside the figure (blue dots). It is most convenient to use it when finding the area of ​​an irregular polygon. However, the greater the arsenal of techniques used, the fewer errors and better results.

Of course, the information given is far from exhausting the types and properties of a trapezoid, as well as methods for finding its area. This article provides an overview of its most important characteristics. In solving geometric problems, it is important to act gradually, start with easy formulas and problems, consistently consolidate understanding, move to a different level of complexity.

Putting together the most common formulas will help students navigate the various ways to calculate the area of ​​​​a trapezoid and better prepare for tests and control work on this topic.

A polygon is a part of a plane bounded by a closed broken line. The corners of a polygon are indicated by the points of the vertices of the polyline. Polygon corner vertices and polygon vertices are congruent points.

Definition. A parallelogram is a quadrilateral whose opposite sides are parallel.

Parallelogram properties

1. Opposite sides are equal.
On fig. eleven AB = CD; BC = AD.

2. Opposite angles are equal (two acute and two obtuse angles).
On fig. 11∠ A = ∠C; ∠B = ∠D.

3 Diagonals (line segments connecting two opposite vertices) intersect and the intersection point is divided in half.

On fig. 11 segments AO = OC; BO = OD.

Definition. A trapezoid is a quadrilateral in which two opposite sides are parallel and the other two are not.

Parallel sides called her grounds, and the other two sides sides.

Types of trapezium

1. Trapeze, whose sides are not equal,
called versatile(Fig. 12).

2. A trapezoid whose sides are equal is called isosceles(Fig. 13).

3. A trapezoid, in which one side makes a right angle with the bases, is called rectangular(Fig. 14).

The segment connecting the midpoints of the sides of the trapezoid (Fig. 15) is called the midline of the trapezoid ( MN). The median line of the trapezoid is parallel to the bases and equal to half their sum.

A trapezoid can be called a truncated triangle (Fig. 17), therefore the names of trapeziums are similar to the names of triangles (triangles are versatile, isosceles, rectangular).

Area of ​​a parallelogram and a trapezoid

Rule. Parallelogram area is equal to the product of its side by the height drawn to this side.

Your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please read our privacy policy and let us know if you have any questions.

Collection and use of personal information

Personal information refers to data that can be used to identify or contact a specific person.

You may be asked to provide your personal information at any time when you contact us.

The following are some examples of the types of personal information we may collect and how we may use such information.

What personal information we collect:

• When you submit an application on the site, we may collect various information, including your name, phone number, address Email etc.

How we use your personal information:

• The personal information we collect allows us to contact you and inform you about unique offers, promotions and other events and upcoming events.
• From time to time, we may use your personal information to send you important notices and communications.
• We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
• If you enter a prize draw, contest or similar incentive, we may use the information you provide to administer such programs.

Disclosure to third parties

We do not disclose information received from you to third parties.

Exceptions:

• In the event that it is necessary - in accordance with the law, judicial order, in legal proceedings, and / or based on public requests or requests from state bodies in the territory of the Russian Federation - disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public interest purposes.
• In the event of a reorganization, merger or sale, we may transfer the personal information we collect to the relevant third party successor.

Protection of personal information

We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as from unauthorized access, disclosure, alteration and destruction.

Maintaining your privacy at the company level

To ensure that your personal information is secure, we communicate privacy and security practices to our employees and strictly enforce privacy practices.

Circumscribed circle and trapezoid. Hello! For you, another publication in which we will consider problems with trapezoids. Assignments are part of the math exam. Here they are combined into a group, not just one trapezoid is given, but a combination of bodies - a trapezoid and a circle. Most of these problems are solved orally. But there are some that need special attention, for example, problem 27926.

What theory should be kept in mind? This is:

Tasks with trapezoids that are available on the blog can be viewed here.

27924. A circle is circumscribed near a trapezoid. The perimeter of the trapezoid is 22, the midline is 5. Find the side of the trapezoid.

Note that a circle can only be circumscribed about an isosceles trapezoid. We are given the middle line, so we can determine the sum of the bases, that is:

So the sum of the sides will be equal to 22–10=12 (perimeter minus the base). Since the sides of an isosceles trapezoid are equal, one side will be equal to six.

27925. Side an isosceles trapezoid is equal to its smaller base, the angle at the base is 60 0, the larger base is 12. Find the radius of the circumscribed circle of this trapezoid.

If you solved problems with a circle and a hexagon inscribed in it, then immediately voice the answer - the radius is 6. Why?

Look: an isosceles trapezoid with a base angle of 60 0 and equal sides AD, DC and CB is half a regular hexagon:

In such a hexagon, the segment connecting opposite vertices passes through the center of the circle. *The center of the hexagon and the center of the circle are the same, more

That is, the larger base of this trapezoid coincides with the diameter of the circumscribed circle. So the radius is six.

*Of course, you can consider the equality of triangles ADO, DOC and OCB. Prove that they are equilateral. Further, conclude that the angle AOB is equal to 180 0 and the point O is equidistant from the vertices A, D, C and B, which means AO=OB=12/2=6.

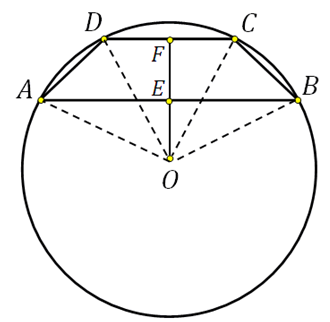
27926. The bases of an isosceles trapezoid are 8 and 6. The radius of the circumscribed circle is 5. Find the height of the trapezoid.

Note that the center of the circumscribed circle lies on the axis of symmetry, and if you build the height of the trapezoid passing through this center, then when it intersects with the bases, it will divide them in half. Let's show this on the sketch, also connect the center to the vertices:

The segment EF is the height of the trapezoid, we need to find it.

In a right triangle OFC we know the hypotenuse (this is the radius of the circle), FC=3 (because DF=FC). Using the Pythagorean theorem, we can calculate OF:

In a right triangle OEB, we know the hypotenuse (this is the radius of the circle), EB=4 (because AE=EB). Using the Pythagorean theorem, we can calculate OE:

Thus EF=FO+OE=4+3=7.

Now an important nuance!

In this problem, the figure clearly shows that the bases lie on opposite sides of the center of the circle, so the problem is solved in this way.

And if the sketch had not been given in the condition?

Then the problem would have two answers. Why? Look carefully - in any circle you can inscribe two trapezoids with given bases:

*That is, given the bases of the trapezium and the radius of the circle, there are two trapezoids.

And the solution will be "second option" will be next.

Using the Pythagorean theorem, we calculate OF:

Let's also calculate OE:

Thus EF=FO–OE=4–3=1.

Of course, in a problem with a short answer to the USE, there cannot be two answers, and a similar problem without a sketch will not be given. Therefore, pay special attention to the sketch! Namely: how the bases of the trapezoid are located. But in tasks with a detailed answer, this was present in past years (with a slightly more complicated condition). Those who considered only one option for the location of the trapezoid lost a point on this task.

27937. A trapezoid is circumscribed about a circle, the perimeter of which is 40. Find its midline.

Here we should immediately recall the property of a quadrilateral circumscribed about a circle:

The sums of the opposite sides of any quadrilateral circumscribed about a circle are equal.

Lesson topic

Trapeze

Lesson Objectives

Continue introducing new definitions in geometry;
To consolidate knowledge about the already studied geometric shapes;
Introduce the formulation and proofs of the properties of a trapezoid;
To teach the use of the properties of various figures in solving problems and performing tasks;
Continue to develop attention in students, logical thinking and mathematical speech;
Cultivate interest in the subject.

Lesson objectives

To arouse interest in knowledge of geometry;
Continue to exercise students in solving problems;
Arouse cognitive interest in the lessons of mathematics.

Lesson plan

1. Repeat the material studied earlier.
2. Acquaintance with the trapezoid, its properties and features.
3. Solving problems and completing tasks.

Repetition of previously studied material

In the previous lesson, you got acquainted with such a figure as a quadrilateral. Let's consolidate the material covered and answer the questions posed:

1. How many angles and sides does a 4-gon have?
2. Formulate the definition of a 4-gon?
3. What is the name of the opposite sides of the 4-gon?
4. What types of quadrangles do you know? List them and define each one.
5. Draw an example of a convex and non-convex quadrilateral.

Trapeze. General properties and definition

A trapezoid is a quadrangular figure in which only one pair of opposite sides is parallel.

In the geometric definition, a trapezoid is a 4-gon that has two parallel sides, and the other two do not.

The name of such an unusual figure as "trapeze" comes from the word "trapezion", which, translated from Greek, means the word "table", from which the word "meal" and other related words also originated.

In some cases in a trapezoid, a pair of opposite sides is parallel, while its other pair is not parallel. In this case, the trapezoid is called curvilinear.

Trapeze elements

The trapezoid consists of such elements as the base, side lines, middle line and its height.

The base of a trapezoid is called its parallel sides;
The lateral sides are called the other two sides of the trapezoid, which are not parallel;
The midline of a trapezoid is called a segment that connects the midpoints of its sides;
The height of a trapezoid is the distance between its bases.

Types of trapezium

Exercise:

1. Formulate the definition of an isosceles trapezoid.
2. What trapezoid is called rectangular?
3. What does an acute-angled trapezoid mean?
4. Which trapezoid is obtuse?

General properties of a trapezoid

First, the middle line of the trapezoid is parallel to the base of the figure and is equal to its half-sum;

Secondly, the segment that connects the midpoints of the diagonals of a 4-angled figure is equal to the half-difference of its bases;

Thirdly, in a trapezoid, parallel lines that intersect the sides of the angle of a given figure cut off proportional segments from the sides of the angle.

Fourth, in any type of trapezoid, the sum of the angles adjacent to its side is 180°.

Where else is there a trapezoid

The word "trapezoid" is present not only in geometry, it has a wider application in Everyday life.

We can come across this unusual word while watching sports competitions of gymnasts performing acrobatic exercises on the trapeze. In gymnastics, a trapezoid is called a sports equipment, which consists of a crossbar suspended on two ropes.

Also, this word can be heard while working out in the gym or among people who are engaged in bodybuilding, since the trapezium is not only a geometric figure or an acrobatic sports equipment, but also powerful back muscles that are located behind the neck.

The figure shows an aerial trapeze, which was invented for circus acrobats by artist Julius Leotard back in the nineteenth century in France. At first, the creator of this number set his projectile at a low height, but in the end it was moved under the very dome of the circus.

Aerialists in the circus perform tricks of flights from trapeze to trapeze, perform cross flights, do somersaults in the air.

In equestrian sport, trapezoid is a stretching exercise or stretching of the horse's body, which is very beneficial and pleasant for the animal. During the horse's stance in the trapezoid position, stretching the legs of the animal or the muscles of its back works. This is beautiful exercise we can observe during the bow or the so-called "front crunch" when the horse is deeply arched.

Task: Give your examples of where else in everyday life you can hear the words "trapeze"?

Did you know that for the first time in 1947, the famous French fashion designer Christian Dior produced a fashion show in which there was a silhouette of an A-line skirt. And although more than sixty years have passed, this silhouette is still in fashion, and does not lose its relevance to this day.

In the wardrobe of the English queen, the A-line skirt has become an indispensable item and her hallmark.

Reminiscent of the geometric shape of a trapezoid, the skirt of the same name goes well with any blouses, blouses, tops and jackets. The classic and democratic style of this popular style allows you to wear it with strict jackets and slightly frivolous tops. In such a skirt it would be appropriate to appear both in the office and at a disco.

Problems with a trapezoid

To facilitate solving problems with trapezoids, it is important to remember a few basic rules:

First, draw two heights: BF and CK.

In one of the cases, as a result you will get a rectangle - ВСФК from which it is clear that FC=BC.

AD=AF+FK+KD, hence AD=AF+BC+KD.

In addition, it is immediately obvious that ABF and DCK are right triangles.

Another option is possible when the trapezoid is not quite standard, where

AD=AF+FD=AF+FK–DK=AF+BC–DK.

But the easiest option is if our trapezoid is isosceles. Then it becomes even easier to solve the problem, because ABF and DCK are right triangles, and they are equal. AB = CD, since the trapezoid is isosceles, and BF = CK, as the height of the trapezoid. From the equality of triangles follows the equality of the corresponding sides.