The function is called increasing on the interval
, if for any points

the inequality
(greater value argument corresponds to the larger value of the function).

Likewise, the function
called decreasing on the interval
, if for any points
from this interval under the condition
the inequality
(a larger value of the argument corresponds to a smaller value of the function).

Increasing on the interval
and decreasing on the interval
functions are called monotonic on the interval
.

Knowing the derivative of a differentiable function allows us to find intervals of its monotonicity.

Theorem (sufficient condition for the function to increase).
functions
positive on the interval
, then the function
increases monotonically over this interval.

Theorem (sufficient condition for a function to decrease). If the derivative is differentiable on the interval
functions
negative on the interval
, then the function
decreases monotonically on this interval.

geometric sense of these theorems is that on the intervals of decreasing function, the functions tangent to the graph form with the axis
obtuse angles, and at intervals of increase - sharp (see Fig. 1).

Theorem (necessary condition for monotonicity of a function). If the function
differentiable and
(
) on the interval
, then it does not decrease (does not increase) on this interval.

Algorithm for finding intervals of monotonicity of a function
:

Example. Find monotonicity intervals of a function
.

Dot called maximum point of the function

such that for everyone , satisfying the condition
, the inequality
.

Feature Maximum is the value of the function at the maximum point.

Figure 2 shows an example of a graph of a function that has maxima at points
.

Dot called minimum point of the function
if there is some number
such that for everyone , satisfying the condition
, the inequality
. Fig. 2 function has a minimum at a point .

There is a common name for highs and lows - extremes . Accordingly, the maximum and minimum points are called extremum points .

A function defined on a segment can have a maximum and minimum only at points inside this segment. It is also impossible to confuse the maximum and minimum of a function with its maximum and minimum values ​​on a segment - these are fundamentally different concepts.

At extreme points, the derivative has special properties.

Theorem (necessary condition for an extremum). Let at the point function
has an extremum. Then either
does not exist, or
.

Those points from the domain of the function, at which
does not exist or in which
, are called critical points of the function .

Thus, the extremum points lie among the critical points. In the general case, the critical point does not have to be an extremum point. If the derivative of a function at some point is equal to zero, then this does not mean that the function has an extremum at this point.

Example. Consider
. We have
, but dot
is not an extremum point (see Figure 3).

Theorem (the first sufficient condition for an extremum). Let at the point function
continuous, and the derivative
when passing through a point changes sign. Then – extremum point: maximum, if the sign changes from “+” to “–”, and minimum, if from “–” to “+”.

If, when passing through a point derivative does not change sign, then at the point there is no extremum.

Theorem (the second sufficient condition for an extremum). Let at the point derivative of a twice differentiable function
equals zero (
), and its second derivative at this point is nonzero (
) and is continuous in some neighborhood of the point . Then - extremum point
; at
is the minimum point, and
this is the maximum point.

Algorithm for finding extremums of a function using the first sufficient extremum condition:

Find derivative.

Find critical points of the function.

Examine the sign of the derivative to the left and right of each critical point and draw a conclusion about the presence of extrema.

Find the extreme values ​​of the function.

Algorithm for finding extrema of a function using the second sufficient extremum condition:

Example. Find extrema of a function
.

Increasing, decreasing and extrema of a function

Finding intervals of increase, decrease and extrema of a function is like independent task, and the most important part of other tasks, in particular, full function study. Initial information about the increase, decrease and extrema of the function are given in theoretical chapter on the derivative, which I highly recommend for preliminary study (or repetition)- also for the reason that the following material is based on the very the essence of the derivative being a harmonious continuation of this article. Although, if time is running out, then a purely formal working out of examples of today's lesson is also possible.

And today there is a spirit of rare unanimity in the air, and I can directly feel that all those present are burning with desire learn to explore a function using a derivative. Therefore, reasonable good eternal terminology immediately appears on the screens of your monitors.

What for? One of the most practical reasons is: to make it clear what is generally required of you in a particular task!

Function monotonicity. Extremum points and function extrema

Let's consider some function . Simplistically, we assume that continuous on the entire number line:

Just in case, we will immediately get rid of possible illusions, especially for those readers who have recently become acquainted with intervals of sign constancy of the function. Now us NOT INTERESTED, how the graph of the function is located relative to the axis (above, below, where it crosses the axis). For persuasiveness, mentally erase the axes and leave one graph. Because the interest is in it.

Function increases on an interval if for any two points of this interval related by the relation , the inequality is true. That is, a larger value of the argument corresponds to a larger value of the function, and its graph goes “from bottom to top”. The demo function grows over the interval .

Likewise, the function decreasing on an interval if for any two points of the given interval, such that , the inequality is true. That is, a larger value of the argument corresponds to a smaller value of the function, and its graph goes “from top to bottom”. Our function is decreasing over the intervals .

If a function is increasing or decreasing over an interval, then it is called strictly monotonous on this interval. What is monotonicity? Take it literally - monotony.

It is also possible to define non-decreasing function (relaxed condition in the first definition) and non-increasing function (softened condition in the 2nd definition). A non-decreasing or non-increasing function on an interval is called a monotonic function on a given interval (strict monotonicity is a special case of "just" monotonicity).

The theory also considers other approaches to determining the increase / decrease of a function, including on half-intervals, segments, but in order not to pour oil-oil-oil on your head, we agree to operate with open intervals with categorical definitions - this is clearer, and for solving many practical problems quite enough.

In this way, in my articles, the wording “monotonicity of a function” will almost always hide intervals strict monotony(strict increase or strict decrease of the function).

Point neighborhood. Words after which the students scatter wherever they can, and hide in horror in the corners. …Although after the post Cauchy limits they probably don’t hide anymore, but only shudder slightly =) Don’t worry, now there will be no proofs of theorems of mathematical analysis - I needed the neighborhood to formulate definitions more rigorously extremum points. We remember:

Neighborhood point name the interval that contains the given point, while for convenience the interval is often assumed to be symmetrical. For example, a point and its standard neighborhood:

Basically the definitions:

The point is called strict maximum point, if exists her neighborhood, for all values ​​of which, except for the point itself, the inequality is fulfilled. In our specific example this is a dot.

The point is called strict minimum point, if exists her neighborhood, for all values ​​of which, except for the point itself, the inequality is fulfilled. In the drawing - point "a".

Note : the requirement that the neighborhood be symmetrical is not necessary at all. In addition, it is important the very fact of existence neighborhood (albeit tiny, even microscopic) that satisfies the specified conditions

Dots are called points of strict extremum or simply extremum points functions. That is, it is a generalized term for maximum points and minimum points.

How to understand the word "extreme"? Yes, just as directly as monotony. Extreme points of the roller coaster.

As in the case of monotonicity, in the theory there are and even more common non-strict postulates (under which, of course, the considered strict cases fall!):

The point is called maximum point, if exists its surroundings, such that for all
The point is called minimum point, if exists its surroundings, such that for all values ​​of this neighborhood, the inequality holds.

Note that according to the last two definitions, any point of a constant function (or a “flat area” of some function) is considered both a maximum point and a minimum point! The function , by the way, is both non-increasing and non-decreasing, that is, monotonic. However, we leave these arguments to theorists, since in practice we almost always contemplate the traditional "hills" and "hollows" (see drawing) with a unique "king of the hill" or "marsh princess". As a variety, it occurs point, directed up or down, for example, the minimum of the function at the point .

Oh, by the way, oh royalty:
- the meaning is called maximum functions;
- the meaning is called minimum functions.

Common name - extremes functions.

Please be careful with your words!

extremum points are "x" values.
Extremes- "game" values.

! Note : sometimes the listed terms refer to the points "x-y" that lie directly on the GRAPH of the function.

How many extrema can a function have?

None, 1, 2, 3, … etc. to infinity. For example, the sine has an infinite number of minimums and maximums.

IMPORTANT! The term "maximum function" not identical term "maximum value of a function". It is easy to see that the value is maximum only in the local neighborhood, and there are “more abruptly comrades” in the upper left. Likewise, "minimum function" is not the same as "minimum function value", and in the drawing we can see that the value is minimum only in a certain area. In this regard, extreme points are also called local extremum points, and the extrema local extremes. They walk and wander around and global brethren. So, any parabola has at its vertex global minimum or global maximum. Further, I will not distinguish between types of extremes, and the explanation is voiced more for general educational purposes - the additional adjectives "local" / "global" should not be taken by surprise.

Let's summarize our short digression into the theory with a control shot: what does the task “find the intervals of monotonicity and the extremum points of the function” imply?

The formulation prompts to find:

- intervals of increase / decrease of the function (non-decreasing, non-increasing appear much less often);

– maximum points and/or minimum points (if any). Well, it’s better to find the minima / maxima themselves from the failure ;-)

How to define all this? With the help of a derivative function!

How to find intervals of increase, decrease,
extremum points and extremums of the function?

Many rules, in fact, are already known and understood from lesson about the meaning of the derivative.

Tangent derivative bears the good news that the function is increasing throughout domains.

With cotangent and its derivative the situation is exactly the opposite.

The arcsine grows on the interval - the derivative is positive here: .
For , the function is defined but not differentiable. However, at the critical point there is a right-hand derivative and a right-hand tangent, and on the other edge, their left-hand counterparts.

I think it will not be difficult for you to carry out similar reasoning for the arc cosine and its derivative.

All of these cases, many of which are tabular derivatives, I remind you, follow directly from definitions of the derivative.

Why explore a function with a derivative?

To get a better idea of ​​what the graph of this function looks like: where it goes "from the bottom up", where it goes "from the top down", where it reaches the lows of the highs (if at all). Not all functions are so simple - in most cases, we have no idea at all about the graph of a particular function.

It is time to move on to more meaningful examples and consider algorithm for finding intervals of monotonicity and extrema of a function:

Example 1

Find increasing/decreasing intervals and extrema of a function

Solution:

1) The first step is to find function scope, and also take note of the breakpoints (if they exist). In this case, the function is continuous on the entire real line, and this action is somewhat formal. But in some cases, serious passions flare up here, so let's treat the paragraph without neglect.

2) The second point of the algorithm is due

necessary condition for an extremum:

If there is an extremum at the point, then either the value does not exist.

Confused by the ending? Extremum of the function "modulo x" .

condition is necessary, but not enough, and the converse is not always true. So, it does not yet follow from equality that the function reaches a maximum or minimum at the point . A classic example has already been lit up above - this is a cubic parabola and its critical point.

But be that as it may, necessary condition extremum dictates the need to find suspicious points. To do this, find the derivative and solve the equation:

At the beginning of the first article about function graphs I told you how to quickly build a parabola using an example : "... we take the first derivative and equate it to zero: ... So, the solution to our equation: - it is at this point that the top of the parabola is located ...". Now, I think, everyone understands why the top of the parabola is exactly at this point =) In general, we should start with a similar example here, but it is too simple (even for a teapot). In addition, there is an analogue at the very end of the lesson about derivative function. So let's raise the level:

Example 2

Find monotonicity intervals and extrema of a function

This is a do-it-yourself example. A complete solution and an approximate finishing sample of the problem at the end of the lesson.

The long-awaited moment of the meeting with fractional rational functions has come:

Example 3

Explore a function using the first derivative

Pay attention to how variantly one and the same task can be reformulated.

Solution:

1) The function suffers infinite breaks at points .

2) We detect critical points. Let's find the first derivative and equate it to zero:

Let's solve the equation. A fraction is zero when its numerator is zero:

Thus, we get three critical points:

3) Set aside ALL detected points on the number line and interval method define the signs of the DERIVATIVE:

I remind you that you need to take some point of the interval, calculate the value of the derivative in it and determine its sign. It’s more profitable not to even count, but to “estimate” verbally. Take, for example, a point belonging to the interval , and perform the substitution: .

Two "pluses" and one "minus" give a "minus", therefore, which means that the derivative is negative on the entire interval.

The action, as you understand, must be carried out for each of the six intervals. By the way, note that the numerator factor and denominator are strictly positive for any point of any interval, which greatly simplifies the task.

So, the derivative told us that the FUNCTION ITSELF increases by and decreases by . It is convenient to fasten intervals of the same type with the union icon .

At the point the function reaches its maximum:
At the point the function reaches its minimum:

Think about why you can not recalculate the second value ;-)

When passing through a point, the derivative does not change sign, so the function has NO EXTREME there - it both decreased and remained decreasing.

! Let's repeat important point : points are not considered critical - they have a function not determined. Accordingly, here extremums cannot be in principle(even if the derivative changes sign).

Answer: the function increases by and decreases on At the point the maximum of the function is reached: , and at the point - the minimum: .

Knowledge of monotonicity intervals and extrema, coupled with established asymptotes gives a very good idea of appearance function graph. An average person is able to verbally determine that a graph of a function has two vertical asymptotes and an oblique asymptote. Here is our hero:

Try again to correlate the results of the study with the graph of this function.
There is no extremum at the critical point, but there is curve inflection(which, as a rule, happens in similar cases).

Example 4

Find extrema of a function

Example 5

Find monotonicity intervals, maxima and minima of a function

... just some kind of X-in-a-cube Holiday turns out today ....
Soooo, who there in the gallery offered to drink for this? =)

Each task has its own substantive nuances and technical subtleties, which are commented out at the end of the lesson.

To determine the nature of a function and talk about its behavior, it is necessary to find intervals of increase and decrease. This process is called function exploration and plotting. The extremum point is used when finding the largest and smallest values ​​of the function, since they increase or decrease the function from the interval.

This article reveals the definitions, we formulate a sufficient sign of increase and decrease on the interval and the condition for the existence of an extremum. This applies to solving examples and problems. The section on differentiation of functions should be repeated, because when solving it will be necessary to use finding the derivative.

Yandex.RTB R-A-339285-1 Definition 1

The function y = f (x) will increase on the interval x when for any x 1 ∈ X and x 2 ∈ X , x 2 > x 1 the inequality f (x 2) > f (x 1) will be feasible. In other words, a larger value of the argument corresponds to a larger value of the function.

Definition 2

The function y = f (x) is considered to be decreasing on the interval x when for any x 1 ∈ X , x 2 ∈ X , x 2 > x 1 the equality f (x 2) > f (x 1) is considered feasible. In other words, a larger function value corresponds to a smaller argument value. Consider the figure below.

Comment: When the function is definite and continuous at the ends of the ascending and descending interval, i.e. (a; b) where x = a, x = b, the points are included in the ascending and descending interval. This does not contradict the definition, which means that it takes place on the interval x.

The main properties of elementary functions of the type y = sin x are definiteness and continuity for real values ​​of the arguments. From here we get that the increase in the sine occurs on the interval - π 2; π 2, then the increase on the segment has the form - π 2; π 2 .

Definition 3

The point x 0 is called maximum point for a function y = f (x) when for all values ​​of x the inequality f (x 0) ≥ f (x) is true. Feature Maximum is the value of the function at the point, and is denoted by y m a x .

The point x 0 is called the minimum point for the function y \u003d f (x) when for all values ​​of x the inequality f (x 0) ≤ f (x) is true. Feature Minimum is the value of the function at the point, and has the notation of the form y m i n .

The neighborhoods of the point x 0 are considered extremum points, and the value of the function that corresponds to the extremum points. Consider the figure below.

Extrema of the function with the largest and smallest value of the function. Consider the figure below.

The first figure says that it is necessary to find the largest value of the function from the segment [ a ; b] . It is found using maximum points and equals the maximum value of the function, and the second figure is more like finding a maximum point at x = b.

Sufficient conditions for increasing and decreasing functions

To find the maxima and minima of a function, it is necessary to apply the signs of an extremum in the case when the function satisfies these conditions. The first feature is the most commonly used.

The first sufficient condition for an extremum

Definition 4

Let a function y = f (x) be given, which is differentiable in the ε neighborhood of the point x 0 , and has continuity at the given point x 0 . Hence we get that

• when f "(x) > 0 with x ∈ (x 0 - ε; x 0) and f" (x)< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• when f"(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >0 for x ∈ (x 0 ; x 0 + ε) , then x 0 is the minimum point.

In other words, we obtain their sign setting conditions:

• when the function is continuous at the point x 0, then it has a derivative with a changing sign, that is, from + to -, which means that the point is called the maximum;
• when the function is continuous at the point x 0, then it has a derivative with a changing sign from - to +, which means that the point is called a minimum.

To correctly determine the maximum and minimum points of the function, you must follow the algorithm for finding them:

• find the domain of definition;
• find the derivative of the function on this area;
• identify zeros and points where the function does not exist;
• determining the sign of the derivative on intervals;
• select the points where the function changes sign.

Consider the algorithm on the example of solving several examples of finding the extrema of the function.

Example 1

Find the maximum and minimum points of the given function y = 2 (x + 1) 2 x - 2 .

Solution

The domain of this function is all real numbers except x = 2. First, we find the derivative of the function and get:

y "= 2 x + 1 2 x - 2" = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2) " (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2) ) - (x + 2) 2 (x - 2) 2 = = 2 (x + 1) (x - 5) (x - 2) 2

From here we see that the zeros of the function are x \u003d - 1, x \u003d 5, x \u003d 2, that is, each bracket must be equated to zero. Mark on the number line and get:

Now we determine the signs of the derivative from each interval. It is necessary to select a point included in the interval, substitute it into the expression. For example, points x = - 2, x = 0, x = 3, x = 6.

We get that

y "(- 2) \u003d 2 (x + 1) (x - 5) (x - 2) 2 x \u003d - 2 \u003d 2 (- 2 + 1) (- 2 - 5) (- 2 - 2) 2 \u003d 2 7 16 \u003d 7 8 > 0, therefore, the interval - ∞; - 1 has a positive derivative. Similarly, we obtain that

y "(0) = 2 (0 + 1) 0 - 5 0 - 2 2 = 2 - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

Since the second interval turned out less than zero, so the derivative on the segment will be negative. The third with a minus, the fourth with a plus. To determine continuity, it is necessary to pay attention to the sign of the derivative, if it changes, then this is an extremum point.

We get that at the point x = - 1 the function will be continuous, which means that the derivative will change sign from + to -. According to the first sign, we have that x = - 1 is the maximum point, which means we get

y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0

The point x = 5 indicates that the function is continuous, and the derivative will change sign from - to +. Hence, x=-1 is the minimum point, and its finding has the form

y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24

Graphic image

Answer: y m a x = y (- 1) = 0 , y m i n = y (5) = 24 .

It is worth paying attention to the fact that the use of the first sufficient sign of an extremum does not require the function to be differentiable from the point x 0 , and this simplifies the calculation.

Example 2

Find the maximum and minimum points of the function y = 1 6 x 3 = 2 x 2 + 22 3 x - 8 .

Solution.

The domain of a function is all real numbers. This can be written as a system of equations of the form:

1 6 x 3 - 2 x 2 - 22 3 x - 8 , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

Then you need to find the derivative:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

The point x = 0 has no derivative, because the values ​​of the one-sided limits are different. We get that:

lim y "x → 0 - 0 = lim yx → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 lim y "x → 0 + 0 = lim yx → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3

It follows that the function is continuous at the point x = 0, then we calculate

lim yx → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 (0 - 0) 3 - 2 (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 lim yx → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 (0 + 0) 2 + 22 3 (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 0 3 - 2 0 2 + 22 3 0 - 8 = - 8

It is necessary to perform calculations to find the value of the argument when the derivative becomes zero:

1 2 x 2 - 4 x - 22 3 , x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0

All points obtained must be marked on the line to determine the sign of each interval. Therefore, it is necessary to calculate the derivative at arbitrary points for each interval. For example, we can take points with values ​​x = - 6 , x = - 4 , x = - 1 , x = 1 , x = 4 , x = 6 . We get that

y " (- 6) \u003d - 1 2 x 2 - 4 x - 22 3 x \u003d - 6 \u003d - 1 2 - 6 2 - 4 (- 6) - 22 3 \u003d - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y "(- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 (- 1) 2 - 4 (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

The image on a straight line has the form

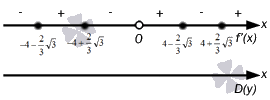
So, we come to the point that it is necessary to resort to the first sign of an extremum. We calculate and get that

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , then from here the maximum points have the values ​​x = - 4 + 2 3 3 , x = 4 - 2 3 3

Let's move on to calculating the minimums:

ymin = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 ymin = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 ymin = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

Let us calculate the maxima of the function. We get that

ymax = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 ymax = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

Graphic image

Answer:

ymin = y - 4 - 2 3 3 = - 8 27 3 ymin = y (0) = - 8 ymin = y 4 + 2 3 3 = - 8 27 3 ymax = y - 4 + 2 3 3 = 8 27 3 ymax = y 4 - 2 3 3 = 8 27 3

If the function f "(x 0) = 0 is given, then with its f "" (x 0) > 0 we get that x 0 is the minimum point if f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

Example 3

Find the maxima and minima of the function y = 8 x x + 1 .

Solution

First, we find the domain of definition. We get that

D (y) : x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

It is necessary to differentiate the function, after which we get

y "= 8 xx + 1" = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x

When x = 1, the derivative becomes equal to zero, which means that the point is a possible extremum. For clarification, it is necessary to find the second derivative and calculate the value at x \u003d 1. We get:

y "" = 4 - x + 1 (x + 1) 2 x " = = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x "(x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2" x + (x + 1) 2 x "(x + 1) 4 x == 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1)" x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 - 4 8 = - 1< 0

Hence, using the 2 sufficient condition for the extremum, we obtain that x = 1 is the maximum point. Otherwise, the entry is y m a x = y (1) = 8 1 1 + 1 = 4 .

Graphic image

Answer: y m a x = y (1) = 4 ..

Definition 5

The function y = f (x) has its derivative up to the nth order in the ε neighborhood of the given point x 0 and its derivative up to the n + 1st order at the point x 0 . Then f "(x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0 .

It follows that when n is an even number, then x 0 is considered an inflection point, when n is an odd number, then x 0 is an extremum point, and f (n + 1) (x 0) > 0, then x 0 is a minimum point, f(n+1)(x0)< 0 , тогда x 0 является точкой максимума.

Example 4

Find the maximum and minimum points of the function y y = 1 16 (x + 1) 3 (x - 3) 4 .

Solution

The original function is an entire rational one, hence it follows that the domain of definition is all real numbers. The function needs to be differentiated. We get that

y "= 1 16 x + 1 3" (x - 3) 4 + (x + 1) 3 x - 3 4 " == 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

This derivative will go to zero at x 1 = - 1, x 2 = 5 7, x 3 = 3. That is, the points can be points of a possible extremum. It is necessary to apply the third sufficient extremum condition. Finding the second derivative allows you to accurately determine the presence of a maximum and minimum of a function. The second derivative is calculated at the points of its possible extremum. We get that

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

This means that x 2 \u003d 5 7 is the maximum point. Applying 3 sufficient criterion, we obtain that for n = 1 and f (n + 1) 5 7< 0 .

It is necessary to determine the nature of the points x 1 = - 1, x 3 = 3. To do this, you need to find the third derivative, calculate the values ​​at these points. We get that

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " == 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

Hence, x 1 = - 1 is the inflection point of the function, since for n = 2 and f (n + 1) (- 1) ≠ 0. It is necessary to investigate the point x 3 = 3 . To do this, we find the 4th derivative and perform calculations at this point:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " == 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0

From the above, we conclude that x 3 \u003d 3 is the minimum point of the function.

Graphic image

Answer: x 2 \u003d 5 7 is the maximum point, x 3 \u003d 3 - the minimum point of the given function.

If you notice a mistake in the text, please highlight it and press Ctrl+Enter

"Increasing and Decreasing Function"

Lesson Objectives:

1. Learn to find intervals of monotony.

2. The development of mental abilities that provide an analysis of the situation and the development of adequate methods of action (analysis, synthesis, comparison).

3. Formation of interest in the subject.

During the classes

Today we continue to study the application of the derivative and consider the question of its application to the study of functions. Front work

And now let's give some definitions to the properties of the "Brainstorm" function

1. What is called a function?

2. What is the name of the x variable?

3. What is the name of the Y variable?

4. What is the scope of a function?

5. What is a function value set?

6. What is an even function?

7. Which function is called odd?

8. What can be said about the graph of an even function?

9. What can be said about the graph of an odd function?

10. What is an increasing function?

11. What is a decreasing function?

12. What is a periodic function?

Mathematics studies mathematical models. One of the most important mathematical models is a function. Exist different ways function descriptions. Which one is the most obvious?

– Graphic.

- How to build a graph?

- By points.

This method is suitable if you know in advance what the graph looks like. For example, what is the graph of a quadratic function, a linear function, an inverse proportionality, a function y = sinx? (The corresponding formulas are demonstrated, students name the curves that are graphs.)

But what if you want to graph a function or even more complex one? You can find multiple points, but how does the function behave between these points?

Put two points on the board, ask the students to show what the graph “between them” might look like:

To find out how a function behaves, its derivative helps.

Open notebooks, write down the number, class work.

The purpose of the lesson: learn how the graph of a function is related to the graph of its derivative, and learn how to solve problems of two types:

1. According to the graph of the derivative, find the intervals of increase and decrease of the function itself, as well as the extremum points of the function;

2. According to the scheme of signs of the derivative on the intervals, find the intervals of increase and decrease of the function itself, as well as the extremum points of the function.

Such tasks are not in our textbooks, but they are found in the tests of the unified state exam (parts A and B).

Today in the lesson we will consider a small element of the work of the second stage of studying the process, the study of one of the properties of the function - the definition of monotonicity intervals

To solve this problem, we need to recall some of the issues discussed earlier.

So, let's write down the topic of today's lesson: Signs of increasing and decreasing functions.

Signs of increasing and decreasing function:

If the derivative of this function is positive for all values ​​of x in the interval (a; c), i.e. f "(x)\u003e 0, then the function increases in this interval.
If the derivative of this function is negative for all values ​​of x in the interval (a; b), i.e. f "(x)< 0, то функция в этом интервале убывает

The order of finding intervals of monotonicity:

Find the scope of the function.

1. Find the first derivative of a function.

2. decide on the board

Find critical points, investigate the sign of the first derivative in the intervals into which the found critical points divide the domain of the function. Find intervals of monotonicity of functions:

a) domain of definition,

b) find the first derivative:,

c) find the critical points: ; , And

3. We investigate the sign of the derivative in the obtained intervals, the solution is presented in the form of a table.

point to extreme points

Let's look at a few examples of examining a function for increasing and decreasing.

A sufficient condition for the existence of a maximum is to change the sign of the derivative when passing through the critical point from "+" to "-", and for a minimum from "-" to "+". If the derivative does not change sign when passing through the critical point, then there is no extremum at this point

1. Find D(f).

2. Find f "(x).

3. Find stationary points, i.e. points where f"(x) = 0 or f"(x) does not exist.
(The derivative is 0 at the zeros of the numerator, the derivative does not exist at the zeros of the denominator)

4. Locate D(f) and these points on the coordinate line.

5. Determine the signs of the derivative on each of the intervals

6. Apply signs.

7. Write down the answer.

Consolidation of new material.

Students work in pairs and write their solutions in their notebooks.

a) y \u003d x³ - 6 x² + 9 x - 9;

b) y \u003d 3 x² - 5x + 4.

Two people work at the blackboard.

a) y \u003d 2 x³ - 3 x² - 36 x + 40

b) y \u003d x4-2 x³

3.Summary of the lesson

Homework: test (differentiated)

Monotone

Very important property function is its monotonicity. Knowing this property of various special functions, one can determine the behavior of various physical, economic, social and many other processes.

The following types of monotonicity of functions are distinguished:

1) function increases, if on some interval, if for any two points and this interval such that . Those. a larger value of the argument corresponds to a larger value of the function;

2) function decreasing, if on some interval, if for any two points and this interval such that . Those. a larger value of the argument corresponds to a smaller value of the function;

3) function non-decreasing, if on some interval, if for any two points and this interval such that ;

4) function does not increase, if on some interval, if for any two points and this interval such that .

2. For the first two cases, the term "strict monotonicity" is also used.

3. The last two cases are specific and are usually specified as a composition of several functions.

4. Separately, we note that the increase and decrease in the graph of the function should be considered exactly from left to right and nothing else.

2. Even/odd.

The function is called odd, if when the sign of the argument changes, it changes its value to the opposite. The formula for this looks like this . This means that after substituting the minus x values ​​into the function in place of all x's, the function will change its sign. The graph of such a function is symmetrical about the origin.

Examples of odd functions are etc.

For example, the graph is indeed symmetrical about the origin:

The function is called even if changing the sign of the argument does not change its value. The formula for this looks like this. This means that after substituting the minus x values ​​into the function in place of all x's, the function will not change as a result. The graph of such a function is symmetrical about the axis.

Examples of even functions are etc.

For example, let's show the symmetry of the graph about the axis:

If a function does not belong to any of the specified types, then it is called neither even nor odd, or function general view . Such functions do not have symmetry.

Such a function, for example, is the recently considered linear function with a graph:

3. A special property of functions is periodicity.

The fact is that the periodic functions that are considered in the standard school curriculum are only trigonometric functions. We have already spoken about them in detail when studying the corresponding topic.

Periodic function is a function that does not change its value when a certain constant non-zero number is added to the argument.

This minimum number is called function period and are marked with a letter.

The formula for this looks like this:

Let's look at this property on the example of a sine graph:

Recall that the period of the functions and is , and the period of and is .

As we already know, there can be a non-standard period for trigonometric functions with a complex argument. These are functions of the form:

They have the same period. And about functions:

They have the same period.

As you can see, to calculate a new period, the standard period is simply divided by the factor in the argument. It does not depend on other modifications of the function.

Limitation.

Function y=f(x) is called bounded from below on the set X⊂D(f) if there exists a number a such that for any xϵX the inequality f(x)< a.

Function y=f(x) is called bounded from above on the set X⊂D(f) if there exists a number a such that for any xϵX the inequality f(x)< a.

If the interval X is not indicated, then it is considered that the function is limited over the entire domain of definition. A function bounded both above and below is called bounded.

The limitation of the function is easy to read from the graph. It is possible to draw some straight line y=a, and if the function is higher than this straight line, then it is bounded from below.

If below, then respectively above. Below is a graph of a lower bounded function. Graph of a bounded function, guys, try to draw it yourself.

Topic: Properties of functions: intervals of increase and decrease; greatest and smallest value; extremum points (local maximum and minimum), function convexity.

periods of increase and decrease.

On the basis of sufficient conditions (signs) for the increase and decrease of the function, the intervals of increase and decrease of the function are found.

Here are the formulations of the signs of increasing and decreasing functions on the interval:

if the derivative of the function y=f(x) positive for any x from interval X, then the function increases by X;

if the derivative of the function y=f(x) negative for any x from interval X, then the function decreases by X.

Thus, to determine the intervals of increase and decrease of a function, it is necessary:

find the scope of the function;

find the derivative of a function;

solve inequalities and on the domain of definition;