মডুলাস হল অভিব্যক্তির পরম মান। অন্তত একরকম একটি মডিউল মনোনীত করার জন্য, এটি সোজা বন্ধনী ব্যবহার করার প্রথাগত। যে মানটি জোড় বন্ধনীতে আবদ্ধ থাকে সেটি হল মান যা মডিউলে নেওয়া হয়। যেকোন মডিউল সমাধানের প্রক্রিয়ার মধ্যে রয়েছে একই প্রত্যক্ষ বন্ধনী খোলা, যাকে গাণিতিক ভাষায় মডুলার বন্ধনী বলা হয়। তাদের প্রকাশ একটি নির্দিষ্ট সংখ্যক নিয়ম অনুযায়ী ঘটে। এছাড়াও, মডিউলগুলি সমাধান করার ক্রমে, মডিউল বন্ধনীতে থাকা সেই অভিব্যক্তিগুলির মানগুলির সেটও রয়েছে। বেশিরভাগ ক্ষেত্রে, মডিউলটি এমনভাবে প্রসারিত করা হয় যে সাবমডিউলের অভিব্যক্তিটি শূন্যের মান সহ ধনাত্মক এবং ঋণাত্মক উভয় মানই পায়। থেকে বিচ্যুত হলে বৈশিষ্ট্য সেট করুনমডিউল, তারপর প্রক্রিয়ায় মূল অভিব্যক্তি থেকে বিভিন্ন সমীকরণ বা অসমতা সংকলিত হয়, যা তারপর সমাধান করা প্রয়োজন। চলুন জেনে নেওয়া যাক কিভাবে মডিউল সমাধান করা যায়।

সমাধান প্রক্রিয়া

মডিউলটির সমাধান মডিউলটির সাথে মূল সমীকরণ লেখার মাধ্যমে শুরু হয়। একটি মডুলাস দিয়ে কীভাবে সমীকরণগুলি সমাধান করবেন এই প্রশ্নের উত্তর দিতে, আপনাকে এটি সম্পূর্ণরূপে খুলতে হবে। এই ধরনের একটি সমীকরণ সমাধান করতে, মডিউল প্রসারিত করা হয়। সমস্ত মডুলার এক্সপ্রেশন বিবেচনা করা আবশ্যক. এটির সংমিশ্রণে অন্তর্ভুক্ত অজানা পরিমাণের কোন মানগুলি নির্ধারণ করা প্রয়োজন, বন্ধনীতে মডুলার অভিব্যক্তিটি অদৃশ্য হয়ে যায়। এটি করার জন্য, মডুলার বন্ধনীতে অভিব্যক্তিটিকে শূন্যের সাথে সমান করা এবং তারপর ফলাফলের সমীকরণের সমাধান গণনা করা যথেষ্ট। পাওয়া মান রেকর্ড করা আবশ্যক. একইভাবে, আপনাকে এই সমীকরণের সমস্ত মডিউলের জন্য সমস্ত অজানা ভেরিয়েবলের মান নির্ধারণ করতে হবে। এর পরে, অভিব্যক্তিতে ভেরিয়েবলের অস্তিত্বের সমস্ত ক্ষেত্রে সংজ্ঞা এবং বিবেচনার সাথে মোকাবিলা করা প্রয়োজন যখন তারা মান শূন্য থেকে আলাদা। এটি করার জন্য, আপনাকে মূল অসমতার সমস্ত মডিউলের সাথে সামঞ্জস্যপূর্ণ অসমতার কিছু সিস্টেম লিখতে হবে। অসমতাগুলি এমনভাবে রচিত হতে হবে যাতে তারা সংখ্যা রেখায় পাওয়া ভেরিয়েবলের সমস্ত উপলব্ধ এবং সম্ভাব্য মানগুলিকে কভার করে। তারপরে আপনাকে ভিজ্যুয়ালাইজেশনের জন্য এই একই নম্বর লাইনটি আঁকতে হবে, যার উপর ভবিষ্যতে সমস্ত প্রাপ্ত মান রাখতে হবে।

এখন প্রায় সবকিছুই অনলাইনে করা যায়। মডিউল নিয়মের ব্যতিক্রম নয়। আপনি অনেকগুলি আধুনিক সংস্থানগুলির একটিতে এটি অনলাইনে সমাধান করতে পারেন। শূন্য মডিউলে থাকা ভেরিয়েবলের সমস্ত মানগুলি একটি বিশেষ সীমাবদ্ধতা হবে যা সমাধান প্রক্রিয়াতে ব্যবহার করা হবে মডুলার সমীকরণ. মূল সমীকরণে, অভিব্যক্তির চিহ্ন পরিবর্তন করার সময় সমস্ত উপলব্ধ মডুলার বন্ধনীগুলিকে প্রসারিত করতে হবে যাতে পছন্দসই পরিবর্তনশীলের মানগুলি সংখ্যারেখায় দৃশ্যমান সেই মানগুলির সাথে মিলে যায়। ফলাফল সমীকরণ সমাধান করা আবশ্যক. ভেরিয়েবলের মান, যা সমীকরণ সমাধানের সময় প্রাপ্ত হবে, মডিউল নিজেই সেট করা সীমাবদ্ধতার বিরুদ্ধে পরীক্ষা করা আবশ্যক। যদি ভেরিয়েবলের মানটি শর্তটি সম্পূর্ণরূপে সন্তুষ্ট করে তবে এটি সঠিক। সমীকরণটি সমাধান করার সময় যে সমস্ত শিকড় প্রাপ্ত হবে, কিন্তু সীমাবদ্ধতার সাথে খাপ খাবে না, সেগুলি অবশ্যই বাতিল করতে হবে।

আমরা গণিত পছন্দ করি নাতার পেশা, এবং সে আমাদের বেছে নেয়।

রাশিয়ান গণিতবিদ Yu.I. মানিন

মডুলো সমীকরণ

স্কুলের গণিতে সমাধান করা সবচেয়ে কঠিন সমস্যা হল মডিউল চিহ্নের অধীনে ভেরিয়েবল সমন্বিত সমীকরণ। এই ধরনের সমীকরণ সফলভাবে সমাধান করার জন্য, মডিউলটির সংজ্ঞা এবং মৌলিক বৈশিষ্ট্যগুলি জানা প্রয়োজন। স্বাভাবিকভাবেই, শিক্ষার্থীদের এই ধরণের সমীকরণ সমাধান করার দক্ষতা থাকতে হবে।

মৌলিক ধারণা এবং বৈশিষ্ট্য

একটি বাস্তব সংখ্যার মডুলাস (পরম মান)চিহ্নিত এবং নিম্নরূপ সংজ্ঞায়িত করা হয়:

প্রতি সহজ বৈশিষ্ট্যমডিউল নিম্নলিখিত সম্পর্ক অন্তর্ভুক্ত:

বিঃদ্রঃ, যে কোন সমান ডিগ্রী জন্য শেষ দুটি বৈশিষ্ট্য রাখা.

এছাড়াও, যদি, কোথায়, তারপর এবং

আরো জটিল মডিউল বৈশিষ্ট্য, যা কার্যকরভাবে মডিউল সহ সমীকরণ সমাধানে ব্যবহার করা যেতে পারে, নিম্নলিখিত উপপাদ্য মাধ্যমে প্রণয়ন করা হয়:

উপপাদ্য ঘ.কোনো বিশ্লেষণমূলক ফাংশন জন্যএবং অসমতা

উপপাদ্য 2।সমতা বৈষম্যের সমান।

উপপাদ্য 3.সমতা অসমতার সমতুল্য.

"সমীকরণ" বিষয়ে সমস্যা সমাধানের সাধারণ উদাহরণ বিবেচনা করুন, মডিউল চিহ্নের অধীনে ভেরিয়েবল ধারণ করে।

মডুলাস দিয়ে সমীকরণ সমাধান করা

একটি মডুলাস দিয়ে সমীকরণ সমাধানের জন্য স্কুলের গণিতের সবচেয়ে সাধারণ পদ্ধতি হল পদ্ধতি, মডিউল সম্প্রসারণের উপর ভিত্তি করে। এই পদ্ধতিটি জেনেরিক, যাইহোক, সাধারণ ক্ষেত্রে, এর প্রয়োগ খুব কষ্টকর গণনার দিকে নিয়ে যেতে পারে। এ বিষয়ে শিক্ষার্থীদেরও অন্যদের সচেতন হতে হবে, আরো কার্যকর পদ্ধতিএবং এই ধরনের সমীকরণ সমাধানের পদ্ধতি। নির্দিষ্টভাবে, উপপাদ্য প্রয়োগ করার দক্ষতা থাকতে হবে, এই নিবন্ধে দেওয়া.

উদাহরণ 1সমীকরণটি সমাধান করুন। (এক)

সমাধান। সমীকরণ (1) "শাস্ত্রীয়" পদ্ধতি দ্বারা সমাধান করা হবে - মডিউল সম্প্রসারণ পদ্ধতি। এটি করার জন্য, আমরা সংখ্যাসূচক অক্ষ ভাঙ্গাবিন্দু এবং ব্যবধান এবং তিনটি ক্ষেত্রে বিবেচনা করুন।

1. যদি , তাহলে , , , এবং সমীকরণ (1) রূপ নেয়। এটি এখান থেকে অনুসরণ করে। যাইহোক, এখানে , তাই পাওয়া মানটি সমীকরণের মূল নয় (1)।

2. যদি, তারপর সমীকরণ (1) থেকে আমরা পাইঅথবা

তখন থেকে সমীকরণের মূল (1)।

3. যদি, তারপর সমীকরণ (1) রূপ নেয়অথবা মনে রাখবেন যে .

উত্তর: , .

মডিউলের সাথে নিম্নলিখিত সমীকরণগুলি সমাধান করার সময়, আমরা এই ধরনের সমীকরণগুলি সমাধান করার দক্ষতা বাড়াতে সক্রিয়ভাবে মডিউলগুলির বৈশিষ্ট্যগুলি ব্যবহার করব।

উদাহরণ 2সমীকরণ সমাধান করুন.

সমাধান।যেহেতু এবং তারপর এটি সমীকরণ থেকে অনুসরণ করে. এ প্রসঙ্গে,,,, এবং সমীকরণ হয়ে যায়. এখান থেকে আমরা পাই. কিন্তু, তাই মূল সমীকরণের কোনো শিকড় নেই।

উত্তর: শিকড় নেই।

উদাহরণ 3সমীকরণ সমাধান করুন.

সমাধান।তখন থেকে . যদি, তাহলে, এবং সমীকরণ হয়ে যায়.

এখান থেকে আমরা পাই।

উদাহরণ 4সমীকরণ সমাধান করুন.

সমাধান।আসুন সমীকরণটিকে একটি সমতুল্য আকারে পুনরায় লিখি. (2)

ফলস্বরূপ সমীকরণটি টাইপের সমীকরণের অন্তর্গত।

উপপাদ্য 2 বিবেচনা করে, আমরা বলতে পারি যে সমীকরণ (2) অসমতার সমতুল্য। এখান থেকে আমরা পাই।

উত্তর: .

উদাহরণ 5সমীকরণটি সমাধান করুন।

সমাধান। এই সমীকরণ ফর্ম আছে. তাই, উপপাদ্য 3 অনুযায়ী, এখানে আমাদের অসমতা আছেঅথবা

উদাহরণ 6সমীকরণ সমাধান করুন.

সমাধান।ধরা যাক যে. কারণ , তাহলে প্রদত্ত সমীকরণটি দ্বিঘাত সমীকরণে রূপ নেয়, (3)

কোথায় . যেহেতু সমীকরণ (3) এর একটি একক ধনাত্মক মূল রয়েছেএবং তারপর . এখান থেকে আমরা মূল সমীকরণের দুটি মূল পাই:এবং .

উদাহরণ 7 সমীকরণ সমাধান করুন. (4)

সমাধান। যেহেতু সমীকরণদুটি সমীকরণের সমন্বয়ের সমতুল্য:এবং , তারপর সমীকরণ (4) সমাধান করার সময় দুটি ক্ষেত্রে বিবেচনা করা প্রয়োজন।

1. যদি , তারপর বা .

এখান থেকে আমরা পাই, এবং।

2. যদি , তারপর বা .

তখন থেকে .

উত্তর: , , , .

উদাহরণ 8সমীকরণ সমাধান করুন . (5)

সমাধান।তারপর থেকে এবং এখান থেকে এবং Eq. (5) থেকে এটি অনুসরণ করে এবং , i.e. এখানে আমাদের সমীকরণের একটি সিস্টেম আছে

যাইহোক, সমীকরণের এই সিস্টেমটি অসামঞ্জস্যপূর্ণ।

উত্তর: শিকড় নেই।

উদাহরণ 9 সমীকরণ সমাধান করুন. (6)

সমাধান।যদি আমরা মনোনীত করি এবং সমীকরণ (6) থেকে আমরা প্রাপ্ত করি

অথবা (৭)

যেহেতু সমীকরণ (7) এর ফর্ম আছে, তাই এই সমীকরণটি অসমতার সমতুল্য। এখান থেকে আমরা পাই। তারপর থেকে বা .

উত্তর: .

উদাহরণ 10সমীকরণ সমাধান করুন. (8)

সমাধান।উপপাদ্য 1 অনুসারে, আমরা লিখতে পারি

(9)

সমীকরণ (8) বিবেচনায় নিয়ে, আমরা উপসংহারে পৌঁছেছি যে উভয় অসমতা (9) সমতায় পরিণত হয়, যেমন সমীকরণ একটি সিস্টেম আছে

যাইহোক, উপপাদ্য 3 দ্বারা, উপরের সমীকরণের সিস্টেমটি অসমতার সিস্টেমের সমতুল্য

(10)

আমরা প্রাপ্ত বৈষম্য (10) সিস্টেমের সমাধান. যেহেতু অসমতার সিস্টেম (10) সমীকরণ (8) এর সমতুল্য, তাই মূল সমীকরণের একটি একক মূল রয়েছে।

উত্তর: .

উদাহরণ 11। সমীকরণ সমাধান করুন. (11)

সমাধান।চলুন এবং , তারপর সমীকরণ (11) সমতা বোঝায়।

এই থেকে এটি যে অনুসরণ করে এবং . সুতরাং, এখানে আমাদের অসমতার একটি ব্যবস্থা রয়েছে

এই বৈষম্য ব্যবস্থার সমাধান হচ্ছেএবং .

উত্তর: , .

উদাহরণ 12।সমীকরণ সমাধান করুন. (12)

সমাধান। সমীকরণ (12) মডিউলগুলির ধারাবাহিক প্রসারণের পদ্ধতি দ্বারা সমাধান করা হবে। এটি করার জন্য, বেশ কয়েকটি ক্ষেত্রে বিবেচনা করুন।

1. যদি, তাহলে।

1.1। যদি , তাহলে এবং , .

1.2। যদি, তাহলে. কিন্তু, অতএব, এই ক্ষেত্রে, সমীকরণ (12) এর কোন মূল নেই।

2. যদি, তাহলে।

2.1। যদি , তাহলে এবং , .

2.2। যদি , তারপর এবং .

উত্তর: , , , , .

উদাহরণ 13সমীকরণ সমাধান করুন. (13)

সমাধান।যেহেতু সমীকরণের বাম দিক (13) অ-ঋণাত্মক, তারপর এবং . এই বিষয়ে, , এবং সমীকরণ (13)

রূপ নেয় বা।

জানা গেছে সমীকরণ দুটি সমীকরণের সমন্বয়ের সমতুল্যএবং , সমাধান যা আমরা পেতে, কারণ , তারপর সমীকরণ (13) এর একটি মূল আছে.

উত্তর: .

উদাহরণ 14 সমীকরণের একটি সিস্টেম সমাধান করুন (14)

সমাধান।যেহেতু এবং , তারপর এবং . অতএব, সমীকরণের সিস্টেম (14) থেকে আমরা সমীকরণের চারটি সিস্টেম পাই:

সমীকরণের উপরের সিস্টেমগুলির শিকড়গুলি সমীকরণের সিস্টেমের শিকড় (14)।

উত্তর: ,, , , , , , .

উদাহরণ 15 সমীকরণের একটি সিস্টেম সমাধান করুন (15)

সমাধান।তখন থেকে . এই বিষয়ে, সমীকরণের সিস্টেম (15) থেকে আমরা সমীকরণের দুটি সিস্টেম পাই

সমীকরণের প্রথম সিস্টেমের মূল হল এবং , এবং দ্বিতীয় সমীকরণ সিস্টেম থেকে আমরা পাই এবং .

উত্তর: , , , .

উদাহরণ 16 সমীকরণের একটি সিস্টেম সমাধান করুন (16)

সমাধান।এটি সিস্টেমের প্রথম সমীকরণ (16) থেকে অনুসরণ করে যে .

তখন থেকে . সিস্টেমের দ্বিতীয় সমীকরণ বিবেচনা করুন। যতটুকু, তারপর, এবং সমীকরণ হয়ে যায়, বা

যদি আমরা মান প্রতিস্থাপনসিস্টেমের প্রথম সমীকরণে (16), তারপর, বা

উত্তর: , .

সমস্যা সমাধানের পদ্ধতির গভীর অধ্যয়নের জন্য, সমীকরণের সমাধানের সাথে সম্পর্কিত, মডিউল চিহ্নের অধীনে ভেরিয়েবল ধারণ করে, আপনি সুপারিশকৃত সাহিত্যের তালিকা থেকে টিউটোরিয়ালের পরামর্শ দিতে পারেন।

1. কারিগরি বিশ্ববিদ্যালয়/এড-এ আবেদনকারীদের জন্য গণিতে কাজের সংগ্রহ। এম.আই. স্ক্যানভি। - এম।: বিশ্ব এবং শিক্ষা, 2013। - 608 পি।

2. Suprun V.P. উচ্চ বিদ্যালয়ের শিক্ষার্থীদের জন্য গণিত: কাজ জটিলতা বৃদ্ধি. - এম।: কেডি "লিব্রোকম" / ইউআরএসএস, 2017। - 200 পি।

3. সুপ্রুন ভি.পি. উচ্চ বিদ্যালয়ের শিক্ষার্থীদের জন্য গণিত: সমস্যা সমাধানের জন্য অ-মানক পদ্ধতি। - এম।: কেডি "লিব্রোকম" / ইউআরএসএস, 2017। - 296 পি।

আপনি কি কিছু জানতে চান?

একজন গৃহশিক্ষকের সাহায্য পেতে - নিবন্ধন করুন।

সাইটে, উপাদানের সম্পূর্ণ বা আংশিক অনুলিপি সহ, উৎসের একটি লিঙ্ক প্রয়োজন।

শিক্ষার্থীদের জন্য সবচেয়ে কঠিন বিষয়গুলির মধ্যে একটি হল মডুলাস চিহ্নের অধীনে একটি পরিবর্তনশীল সমীকরণ সমাধান করা। চলুন শুরু করা যাক এটা কিসের সাথে যুক্ত? কেন, উদাহরণস্বরূপ, বেশিরভাগ শিশুরা বাদামের মতো দ্বিঘাত সমীকরণে ক্লিক করে, তবে এই জাতীয় সহ জটিল ধারণাকিভাবে মডিউল এত সমস্যা আছে?

আমার মতে, এই সমস্ত অসুবিধাগুলি একটি মডুলাসের সাথে সমীকরণগুলি সমাধানের জন্য স্পষ্টভাবে প্রণয়নকৃত নিয়মের অভাবের সাথে যুক্ত। সুতরাং, একটি দ্বিঘাত সমীকরণ সমাধান করার সময়, শিক্ষার্থী নিশ্চিতভাবে জানে যে তাকে প্রথমে বৈষম্যমূলক সূত্র প্রয়োগ করতে হবে এবং তারপরে দ্বিঘাত সমীকরণের মূলের জন্য সূত্রগুলি প্রয়োগ করতে হবে। কিন্তু যদি একটি মডিউল সমীকরণের সম্মুখীন হয়? যখন সমীকরণটি মডুলাস চিহ্নের অধীনে একটি অজানা থাকে তখন আমরা প্রয়োজনীয় কর্ম পরিকল্পনাটি স্পষ্টভাবে বর্ণনা করার চেষ্টা করব। আমরা প্রতিটি ক্ষেত্রে বেশ কয়েকটি উদাহরণ দিই।

কিন্তু প্রথম, আসুন মনে রাখবেন মডিউল সংজ্ঞা. সুতরাং, সংখ্যার মডুলাস কসংখ্যা নিজেই যদি বলা হয় কঅ নেতিবাচক এবং -কযদি সংখ্যা ক শূন্যের চেয়ে কম. আপনি এটি এই মত লিখতে পারেন:

|a| = a যদি a ≥ 0 এবং |a| = -a যদি ক< 0

মডিউলটির জ্যামিতিক অর্থ সম্পর্কে বলতে গেলে, এটি মনে রাখা উচিত যে প্রতিটি বাস্তব সংখ্যা সংখ্যা অক্ষের একটি নির্দিষ্ট বিন্দুর সাথে মিলে যায় - এটি সমন্বয় সুতরাং, মডিউল বা একটি সংখ্যার পরম মান হল এই বিন্দু থেকে সাংখ্যিক অক্ষের উৎপত্তি পর্যন্ত দূরত্ব। দূরত্ব সবসময় একটি ধনাত্মক সংখ্যা হিসাবে দেওয়া হয়। সুতরাং, যেকোনো ঋণাত্মক সংখ্যার মডুলাস একটি ধনাত্মক সংখ্যা। যাইহোক, এমনকি এই পর্যায়ে, অনেক শিক্ষার্থী বিভ্রান্ত হতে শুরু করে। যে কোনো সংখ্যা মডিউলে থাকতে পারে, কিন্তু মডিউল প্রয়োগের ফলাফল সর্বদা একটি ধনাত্মক সংখ্যা।

এখন সমীকরণ সমাধানের দিকে এগিয়ে যাওয়া যাক।

1. ফর্মের একটি সমীকরণ বিবেচনা করুন |x| = c, যেখানে c একটি বাস্তব সংখ্যা। এই সমীকরণটি মডুলাসের সংজ্ঞা ব্যবহার করে সমাধান করা যেতে পারে।

আমরা সমস্ত বাস্তব সংখ্যাকে তিনটি গ্রুপে বিভক্ত করি: যেগুলি শূন্যের চেয়ে বড়, যেগুলি শূন্যের চেয়ে কম, এবং তৃতীয় দলটি হল সংখ্যা 0৷ আমরা একটি চিত্রের আকারে সমাধানটি লিখি:

(±c হলে c > 0

যদি |x| = c, তারপর x = (0 হলে c = 0

( সঙ্গে থাকলে শিকড় নেই< 0

1) |x| = 5, কারণ 5 > 0, তারপর x = ±5;

2) |x| = -5, কারণ -5< 0, то уравнение не имеет корней;

3) |x| = 0, তারপর x = 0।

2. ফর্মের একটি সমীকরণ |f(x)| = b, যেখানে b > 0। এই সমীকরণটি সমাধান করার জন্য, মডুলাস থেকে মুক্তি পাওয়া প্রয়োজন। আমরা এটি এভাবে করি: f(x) = b বা f(x) = -b। এখন প্রতিটি প্রাপ্ত সমীকরণ আলাদাভাবে সমাধান করা প্রয়োজন। যদি মূল সমীকরণে খ< 0, решений не будет.

1) |x + 2| = 4, কারণ 4 > 0, তারপর

x + 2 = 4 বা x + 2 = -4

2) |x 2 – 5| = 11, কারণ 11 > 0, তারপর

x 2 - 5 = 11 বা x 2 - 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 কোন শিকড় নেই

3) |x 2 – 5x| = -8, কারণ -আটটি< 0, то уравнение не имеет корней.

3. ফর্মের একটি সমীকরণ |f(x)| = g(x)। মডিউলের অর্থ অনুসারে, এই জাতীয় সমীকরণের সমাধান থাকবে যদি এর ডান দিকটি শূন্যের চেয়ে বড় বা সমান হয়, অর্থাৎ g(x) ≥ 0. তারপর আমাদের আছে:

f(x) = g(x)বা f(x) = -g(x).

1) |2x – 1| = 5x - 10। এই সমীকরণটির মূল থাকবে যদি 5x - 10 ≥ 0 হয়। এখান থেকেই এই ধরনের সমীকরণের সমাধান শুরু হয়।

1. O.D.Z. 5x – 10 ≥ 0

2. সমাধান:

2x - 1 = 5x - 10 বা 2x - 1 = -(5x - 10)

3. O.D.Z একত্রিত করুন এবং সমাধান, আমরা পাই:

মূল x \u003d 11/7 O.D.Z. অনুসারে মাপসই হয় না, এটি 2 এর কম, এবং x \u003d 3 এই শর্তটি পূরণ করে।

উত্তরঃ x = 3

2) |x – 1| \u003d 1 - x 2।

1. O.D.Z. 1 - x 2 ≥ 0. ইন্টারভাল পদ্ধতি ব্যবহার করে এই অসমতা সমাধান করা যাক:

(1 – x)(1 + x) ≥ 0

2. সমাধান:

x - 1 \u003d 1 - x 2 বা x - 1 \u003d - (1 - x 2)

x 2 + x - 2 = 0 x 2 - x = 0

x = -2 বা x = 1 x = 0 বা x = 1

3. সমাধান এবং O.D.Z. একত্রিত করুন:

শুধুমাত্র শিকড় x = 1 এবং x = 0 উপযুক্ত।

উত্তরঃ x = 0, x = 1।

4. ফর্মের একটি সমীকরণ |f(x)| = |g(x)|। এই ধরনের একটি সমীকরণ নিম্নলিখিত দুটি সমীকরণ f(x) = g(x) বা f(x) = -g(x) এর সমতুল্য।

1) |x 2 - 5x + 7| = |2x – 5|। এই সমীকরণটি নিম্নলিখিত দুটির সমতুল্য:

x 2 - 5x + 7 = 2x - 5 বা x 2 - 5x +7 = -2x + 5

x 2 - 7x + 12 = 0 x 2 - 3x + 2 = 0

x = 3 বা x = 4 x = 2 বা x = 1

উত্তরঃ x = 1, x = 2, x = 3, x = 4।

5. প্রতিস্থাপন পদ্ধতি (ভেরিয়েবলের পরিবর্তন) দ্বারা সমাধান করা সমীকরণ। এই পদ্ধতিসমাধান ব্যাখ্যা করা সবচেয়ে সহজ নির্দিষ্ট উদাহরণ. সুতরাং, একটি মডুলাস সহ একটি দ্বিঘাত সমীকরণ দেওয়া যাক:

x 2 – 6|x| + 5 = 0. মডিউল x 2 = |x| এর বৈশিষ্ট্য অনুসারে 2, তাই সমীকরণটি নিম্নরূপ পুনর্লিখন করা যেতে পারে:

|x| 2–6|x| + 5 = 0. আসুন পরিবর্তন করি |x| = t ≥ 0, তাহলে আমাদের থাকবে:

t 2 - 6t + 5 \u003d 0। এই সমীকরণটি সমাধান করে, আমরা t \u003d 1 বা t \u003d 5 পেয়েছি। প্রতিস্থাপনে ফিরে আসা যাক:

|x| = 1 বা |x| = 5

x = ±1 x = ±5

উত্তর: x = -5, x = -1, x = 1, x = 5।

আসুন আরেকটি উদাহরণ দেখি:

x 2 + |x| – 2 = 0. মডিউল x 2 = |x| এর বৈশিষ্ট্য অনুসারে 2, তাই

|x| 2 + |x| – 2 = 0। আসুন পরিবর্তন করি |x| = t ≥ 0, তারপর:

t 2 + t - 2 \u003d 0। এই সমীকরণটি সমাধান করলে, আমরা পাই, t \u003d -2 বা t \u003d 1। আসুন প্রতিস্থাপনে ফিরে যাই:

|x| = -2 বা |x| = 1

কোন শিকড় নেই x = ± 1

উত্তরঃ x = -1, x = 1।

6. অন্য ধরনের সমীকরণ হল "জটিল" মডুলাস সহ সমীকরণ। এই ধরনের সমীকরণগুলির মধ্যে "একটি মডিউলের মধ্যে মডিউল" রয়েছে এমন সমীকরণ অন্তর্ভুক্ত। এই ধরণের সমীকরণগুলি মডিউলের বৈশিষ্ট্যগুলি ব্যবহার করে সমাধান করা যেতে পারে।

1) |3 – |x|| = 4. আমরা দ্বিতীয় প্রকারের সমীকরণের মতো একইভাবে কাজ করব। কারণ 4 > 0, তাহলে আমরা দুটি সমীকরণ পাব:

3 – |x| = 4 বা 3 – |x| =-4।

এখন প্রতিটি সমীকরণে মডিউল x প্রকাশ করা যাক, তারপর |x| = -1 বা |x| = 7।

আমরা প্রতিটি ফলাফলের সমীকরণ সমাধান করি। প্রথম সমীকরণে কোন শিকড় নেই, কারণ -এক< 0, а во втором x = ±7.

উত্তর x = -7, x = 7।

2) |3 + |x + 1|| = 5. আমরা এই সমীকরণটি একইভাবে সমাধান করি:

3 + |x + 1| = 5 বা 3 + |x + 1| =-5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 বা x + 1 = -2। কোন শিকড় আছে.

উত্তরঃ x = -3, x = 1।

একটি মডুলাস দিয়ে সমীকরণ সমাধানের জন্য একটি সর্বজনীন পদ্ধতিও রয়েছে। এটি ব্যবধান পদ্ধতি। তবে আমরা এটি আরও বিবেচনা করব।

সাইটে, উপাদানের সম্পূর্ণ বা আংশিক অনুলিপি সহ, উৎসের একটি লিঙ্ক প্রয়োজন।

MBOU মাধ্যমিক বিদ্যালয় №17 ইভানভ

« মডিউল সমীকরণ»
পদ্ধতিগত বিকাশ

সংকলিত

গণিত শিক্ষক

লেবেদেভা এন.ভি.

20010

ব্যাখ্যামূলক টীকা

অধ্যায় 1 ভূমিকা

বিভাগ 2. প্রধান বৈশিষ্ট্য বিভাগ 3. একটি সংখ্যার মডুলাস ধারণার জ্যামিতিক ব্যাখ্যা বিভাগ 4. ফাংশনের গ্রাফ y = |x| ধারা 5 কনভেনশন

অধ্যায় 2

বিভাগ 1. ফর্মের সমীকরণ |F(х)| = মি (প্রোটোজোয়া) বিভাগ 2. ফর্মের সমীকরণ F(|х|) = m বিভাগ 3. ফর্মের সমীকরণ |F(х)| = G(x) বিভাগ 4. ফর্মের সমীকরণ |F(х)| = ± F(x) (সুন্দর) বিভাগ 5. ফর্মের সমীকরণ |F(х)| = |G(x)| অধ্যায় 6. অ-মানক সমীকরণ সমাধানের উদাহরণ বিভাগ 7. ফর্মের সমীকরণ |F(х)| + |G(x)| = 0 বিভাগ 8. ফর্মের সমীকরণ |а 1 x ± в 1 | ± |a 2 x ± 2 এর মধ্যে | ± …|a n x ± in n | = মি বিভাগ 9. একাধিক মডিউল সমন্বিত সমীকরণ

অধ্যায় 3. একটি মডুলাস দিয়ে বিভিন্ন সমীকরণ সমাধানের উদাহরণ।

বিভাগ 1. ত্রিকোণমিতিক সমীকরণ অধ্যায় 2 সূচকীয় সমীকরণ ধারা 3 লগারিদমিক সমীকরণ বিভাগ 4. অযৌক্তিক সমীকরণ বিভাগ 5. উন্নত জটিলতার কাজ অনুশীলনের উত্তর গ্রন্থপঞ্জি

ব্যাখ্যামূলক টীকা.

একটি বাস্তব সংখ্যার পরম মান (মডুলাস) এর ধারণা তার অপরিহার্য বৈশিষ্ট্যগুলির মধ্যে একটি। এই ধারণাটি শারীরিক, গাণিতিক এবং প্রযুক্তিগত বিজ্ঞানের বিভিন্ন শাখায় ব্যাপকভাবে ব্যবহৃত হয়। রাশিয়ান ফেডারেশনের প্রতিরক্ষা মন্ত্রকের প্রোগ্রাম অনুসারে মাধ্যমিক বিদ্যালয়ে গণিতের পাঠদানের অনুশীলনে, "একটি সংখ্যার পরম মান" ধারণাটি বারবার সম্মুখীন হয়: 6 তম গ্রেডে, একটি মডিউলের সংজ্ঞা। , এর জ্যামিতিক অর্থ, চালু করা হয়; 8 ম শ্রেণীতে, পরম ত্রুটির ধারণা তৈরি হয়, মডুলাস ধারণকারী সহজ সমীকরণ এবং অসমতার সমাধান বিবেচনা করা হয়, পাটিগণিতের বৈশিষ্ট্যগুলি বর্গমূল; 11 তম গ্রেডে, ধারণাটি "রুট" বিভাগে পাওয়া যায় nতম ডিগ্রী।"শিক্ষাদানের অভিজ্ঞতা দেখায় যে শিক্ষার্থীরা প্রায়শই এই উপাদান সম্পর্কে জ্ঞানের প্রয়োজন এমন কাজগুলি সমাধান করতে অসুবিধার সম্মুখীন হয় এবং প্রায়শই সম্পূর্ণ করা শুরু করার আগে এড়িয়ে যায়। 9 তম এবং 11 তম গ্রেডের কোর্সের পরীক্ষার কাজের পাঠ্যগুলিতে, অনুরূপ কাজগুলিও অন্তর্ভুক্ত রয়েছে। এছাড়াও, বিশ্ববিদ্যালয়গুলি স্কুল স্নাতকদের উপর যে প্রয়োজনীয়তাগুলি আরোপ করে তা আলাদা, যথা, আরও৷ উচ্চস্তরস্কুল পাঠ্যক্রমের প্রয়োজনীয়তার চেয়ে। জীবনের জন্য আধুনিক সমাজচিন্তার একটি গাণিতিক শৈলী গঠন খুবই গুরুত্বপূর্ণ, নির্দিষ্ট মানসিক দক্ষতায় উদ্ভাসিত। মডিউলগুলির সাথে সমস্যা সমাধানের প্রক্রিয়াতে, সাধারণীকরণ এবং সংমিশ্রণ, বিশ্লেষণ, শ্রেণিবিন্যাস এবং পদ্ধতিগতকরণ, সাদৃশ্যের মতো কৌশলগুলি প্রয়োগ করার ক্ষমতা প্রয়োজন। এই জাতীয় কাজের সমাধান আপনাকে স্কুল কোর্সের প্রধান বিভাগ, স্তরের জ্ঞান পরীক্ষা করতে দেয় যুক্তিযুক্ত চিন্তা, প্রাথমিক গবেষণা দক্ষতা। এই কাজবিভাগগুলির একটিতে উত্সর্গীকৃত - মডিউল ধারণকারী সমীকরণের সমাধান। এটি তিনটি অধ্যায় নিয়ে গঠিত। প্রথম অধ্যায় মৌলিক ধারণা এবং সবচেয়ে গুরুত্বপূর্ণ তাত্ত্বিক গণনার পরিচয় দেয়। দ্বিতীয় অধ্যায়ে মডিউল সমন্বিত নয়টি মৌলিক ধরনের সমীকরণ প্রস্তাব করা হয়েছে, সেগুলো সমাধানের পদ্ধতি বিবেচনা করা হয়েছে এবং বিভিন্ন স্তরের জটিলতার উদাহরণ বিশ্লেষণ করা হয়েছে। তৃতীয় অধ্যায়টি আরও জটিল এবং অ-মানক সমীকরণ (ত্রিকোণমিতিক, সূচকীয়, লগারিদমিক এবং অযৌক্তিক) প্রস্তাব করে। প্রতিটি ধরণের সমীকরণের জন্য স্বাধীন সমাধানের জন্য অনুশীলন রয়েছে (উত্তর এবং নির্দেশাবলী সংযুক্ত)। এই কাজের মূল উদ্দেশ্য হল শিক্ষকদের পাঠের প্রস্তুতি এবং ঐচ্ছিক কোর্সের আয়োজনে পদ্ধতিগত সহায়তা প্রদান করা। উপাদান হিসাবে এছাড়াও ব্যবহার করা যেতে পারে শিক্ষার পথপ্রদর্শকউচ্চ বিদ্যালয়ের শিক্ষার্থীদের জন্য। কাজের প্রস্তাবিত কাজগুলি আকর্ষণীয় এবং সমাধান করা সর্বদা সহজ নয়, যা শিক্ষার্থীদের শেখার অনুপ্রেরণাকে আরও সচেতন করা, তাদের দক্ষতা পরীক্ষা করা এবং বিশ্ববিদ্যালয়গুলিতে প্রবেশের জন্য স্কুল স্নাতকদের প্রস্তুতির স্তর উন্নত করা সম্ভব করে তোলে। প্রস্তাবিত ব্যায়ামগুলির একটি বিভেদপূর্ণ নির্বাচন উপাদানের আত্তীকরণের প্রজনন স্তর থেকে সৃজনশীল এক রূপান্তরকে বোঝায়, সেইসাথে অ-মানক সমস্যা সমাধানে কীভাবে তাদের জ্ঞান প্রয়োগ করতে হয় তা শেখানোর সুযোগ।

অধ্যায় 1 ভূমিকা.

ধারা 1. পরম মান নির্ধারণ .

সংজ্ঞা : একটি বাস্তব সংখ্যার পরম মান (মডুলাস) কএকটি অ-ঋণাত্মক সংখ্যা বলা হয়: কবা -ক উপাধি: │ ক │ এন্ট্রিটি নিম্নরূপ: "ক নম্বরের মডিউল" বা "ক নম্বরের পরম মান"

│ a যদি a > 0

│a│ = │ 0 যদি a = 0 (1)

│ - ক, যদি ক
উদাহরণ: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

এক্সপ্রেশন মডিউল প্রসারিত করুন:

ক) │x - 8│ যদি x > 12 খ) │2x + 3│ যদি x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

বিভাগ 2. মৌলিক বৈশিষ্ট্য।

পরম মানের মৌলিক বৈশিষ্ট্য বিবেচনা করুন। সম্পত্তি #1: বিপরীত সংখ্যার সমান মডিউল আছে, যেমন │а│=│-а│সাম্যের সঠিকতা দেখাই। সংখ্যার সংজ্ঞা লিখি - ক : │- a│= (2) আসুন সেট (1) এবং (2) তুলনা করি। স্পষ্টতই, সংখ্যার পরম মানগুলির সংজ্ঞা কএবং - কমেলে তাই, │а│=│-а│
নিম্নলিখিত বৈশিষ্ট্যগুলি বিবেচনা করার সময়, আমরা নিজেদেরকে তাদের গঠনের মধ্যে সীমাবদ্ধ রাখি, যেহেতু তাদের প্রমাণ দেওয়া আছে সম্পত্তি #2: বাস্তব সংখ্যার একটি সসীম সংখ্যার যোগফলের পরম মান পদগুলির পরম মানের যোগফলকে অতিক্রম করে না: সম্পত্তি #3: দুটি বাস্তব সংখ্যার মধ্যে পার্থক্যের পরম মান তাদের পরম মানের সমষ্টিকে অতিক্রম করে না: │а - в│ ≤│а│+│в│ সম্পত্তি #4: প্রকৃত সংখ্যার একটি সসীম সংখ্যার গুণফলের পরম মান গুণনীয়কগুলির পরম মানের গুণফলের সমান: │а · в│=│а│·│в│ সম্পত্তি #5: বাস্তব সংখ্যার ভাগফলের পরম মান তাদের পরম মানের ভাগফলের সমান:

বিভাগ 3. একটি সংখ্যার মডুলাস ধারণার জ্যামিতিক ব্যাখ্যা।

প্রতিটি বাস্তব সংখ্যা সংখ্যা রেখার একটি বিন্দুর সাথে যুক্ত হতে পারে, যা এই বাস্তব সংখ্যার একটি জ্যামিতিক উপস্থাপনা হবে। সংখ্যা রেখার প্রতিটি বিন্দু উৎপত্তি থেকে তার দূরত্বের সাথে মিলে যায়, অর্থাৎ উৎপত্তি থেকে প্রদত্ত বিন্দু পর্যন্ত সেগমেন্টের দৈর্ঘ্য। এই দূরত্ব সবসময় একটি অ নেতিবাচক মান হিসাবে বিবেচনা করা হয়. অতএব, সংশ্লিষ্ট অংশের দৈর্ঘ্য প্রদত্ত বাস্তব সংখ্যার পরম মানের জ্যামিতিক ব্যাখ্যা হবে

উপস্থাপিত জ্যামিতিক চিত্র স্পষ্টভাবে সম্পত্তি নং 1 নিশ্চিত করে, অর্থাৎ বিপরীত সংখ্যার মডুলি সমান। এখান থেকে, সমতার বৈধতা সহজেই বোঝা যায়: │x - a│= │a - x│। এটি │х│= m সমীকরণটি সমাধান করার জন্য আরও স্পষ্ট হয়ে ওঠে, যেখানে m ≥ 0, যথা x 1.2 = ± m। উদাহরণ: 1) │х│= 4 x 1.2 = ± 4 2) │х - 3│= 1
x 1.2 = 2; 4

বিভাগ 4. ফাংশন y \u003d │х│ এর গ্রাফ

এই ফাংশনের ডোমেইন হল সমস্ত বাস্তব সংখ্যা।

বিভাগ 5. প্রতীক।

ভবিষ্যতে, সমীকরণ সমাধানের উদাহরণগুলি বিবেচনা করার সময়, নিম্নলিখিতগুলি ব্যবহার করা হবে। নিয়মাবলী: ( - সিস্টেম সাইন [ - সেট সাইন সমীকরণের একটি সিস্টেম (অসমতা) সমাধান করার সময়, সিস্টেমে অন্তর্ভুক্ত সমীকরণগুলির (বৈষম্য) সমাধানগুলির ছেদ পাওয়া যায়। সমীকরণের একটি সেট (বৈষম্য) সমাধান করার সময়, সেটে অন্তর্ভুক্ত সমীকরণগুলির (বৈষম্য) সমাধানগুলির একটি মিল খুঁজে পাওয়া যায়।

অধ্যায় 2

এই অধ্যায়ে, আমরা এক বা একাধিক মডিউল সম্বলিত সমীকরণগুলি সমাধান করার বীজগণিতিক উপায়গুলি দেখব।

বিভাগ 1. ফর্মের সমীকরণ │F (х) │= m

এই ধরনের একটি সমীকরণ সহজ বলা হয়. এটির একটি সমাধান আছে যদি এবং শুধুমাত্র যদি m ≥ 0 হয়। মডুলাসের সংজ্ঞা অনুসারে, মূল সমীকরণটি দুটি সমীকরণের সমন্বয়ের সমতুল্য: │ চ(x)│=মি
উদাহরণ:
№1. সমীকরণটি সমাধান করুন: │7x - 2│= 9


উত্তরঃ x 1 = - 1; এক্স 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 \u003d -2 x (x + 3) \u003d 0 x 1 \u003d 0; x 2 = -3 উত্তরঃ শিকড়ের যোগফল - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 বোঝায় x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – উভয় মানই শর্ত পূরণ করে m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 উত্তরঃ সমীকরণের মূল সংখ্যা 7। অনুশীলন:
№1. সমীকরণটি সমাধান করুন এবং মূলের যোগফল নির্দেশ করুন: │x - 5│= 3 №2 . সমীকরণটি সমাধান করুন এবং ছোট মূল নির্দেশ করুন: │x 2 + x │ \u003d 0 №3 . সমীকরণটি সমাধান করুন এবং বড় মূল নির্দেশ করুন: │x 2 - 5x + 4 │ \u003d 4 №4 সমীকরণটি সমাধান করুন এবং সম্পূর্ণ মূল নির্দেশ করুন: │2x 2 - 7x + 6│ \u003d 1 №5 সমীকরণটি সমাধান করুন এবং মূল সংখ্যা নির্দেশ করুন: │x 4 - 13x 2 + 50 │ = 14

বিভাগ 2. ফর্মের সমীকরণ F(│х│) = m

বাম দিকের ফাংশন আর্গুমেন্টটি মডুলো চিহ্নের অধীনে, যখন ডান দিকটি পরিবর্তনশীল থেকে স্বাধীন। আসুন এই ধরণের সমীকরণ সমাধানের দুটি উপায় বিবেচনা করি। 1 উপায়:পরম মানের সংজ্ঞা অনুসারে, মূল সমীকরণটি দুটি সিস্টেমের সামগ্রিকতার সমতুল্য। যার প্রতিটিতে সাবমডিউল এক্সপ্রেশনে একটি শর্ত আরোপ করা হয়। চ(│х│) =মি
যেহেতু F(│х│) ফাংশনটি এমনকি সংজ্ঞার সম্পূর্ণ ডোমেনে রয়েছে, তাই সমীকরণের মূলগুলি F(х) = m এবং F(-х) = m হল বিপরীত সংখ্যার জোড়া৷ অতএব, এটি একটি সিস্টেমের সমাধান করার জন্য যথেষ্ট (এইভাবে উদাহরণগুলি বিবেচনা করার সময়, একটি সিস্টেমের সমাধান দেওয়া হবে)। ২টি পথ:একটি নতুন পরিবর্তনশীল প্রবর্তনের পদ্ধতির প্রয়োগ। এই ক্ষেত্রে, উপাধি │х│= a চালু করা হয়েছে, যেখানে a ≥ 0। এই পদ্ধতিডিজাইনে কম বিশাল।
উদাহরণ: №1 . সমীকরণটি সমাধান করুন: 3x 2 - 4│x│ = - 1 একটি নতুন চলকের ভূমিকা ব্যবহার করা যাক। │x│= a নির্দেশ করুন, যেখানে a ≥ 0। আমরা 3a 2 - 4a + 1 = 0 D = 16 - 12 = 4 a 1 = 1 a 2 = 1 / 3 সমীকরণটি পাই আমরা মূল চলকটিতে ফিরে আসি: │x │ = 1 এবং │х│= 1/3। প্রতিটি সমীকরণের দুটি মূল রয়েছে। উত্তরঃ x 1 = 1; এক্স 2 = - 1; এক্স 3 = 1 / 3 ; এক্স 4 = - 1 / 3 . №2. সমীকরণটি সমাধান করুন: 5x 2 + 3│x│- 1 \u003d 1 / 2 │x│ + 3x 2
প্রথম সেট সিস্টেমের সমাধান বের করা যাক: 4x 2 + 5x - 2 \u003d 0 D \u003d 57 x 1 \u003d -5 + √57 / 8 x 2 \u003d -5-√57 / 8 মনে রাখবেন যে x 2 করে শর্ত x ≥ 0 সন্তুষ্ট নয়। সমাধান দ্বারা দ্বিতীয় সিস্টেমটি বিপরীত সংখ্যা x 1 হবে। উত্তরঃ x 1 = -5+√57 / 8 ; এক্স 2 = 5-√57 / 8 .№3 . সমীকরণটি সমাধান করুন: x 4 - │х│= 0 বোঝান │х│= a, যেখানে a ≥ 0। আমরা একটি 4 - a \u003d 0 a (a 3 - 1) \u003d 0 a 1 \u003d 0 পাই a 2 \u003d 1 আমরা মূল ভেরিয়েবলে ফিরে আসি: │х│=0 এবং │х│= 1 x = 0; ± 1 উত্তরঃ x 1 = 0; এক্স 2 = 1; এক্স 3 = - 1.
অনুশীলন: №6. সমীকরণটি সমাধান করুন: 2│х│ - 4.5 = 5 - 3/8 │х│ №7 . সমীকরণটি সমাধান করুন, উত্তরে মূল সংখ্যা নির্দেশ করুন: 3x 2 - 7│x│ + 2 = 0 №8 . সমীকরণটি সমাধান করুন, উত্তরে সম্পূর্ণ সমাধানগুলি নির্দেশ করুন: x 4 + │х│ - 2 = 0

বিভাগ 3. ফর্মের সমীকরণ │F(х)│ = G(х)

এই ধরনের একটি সমীকরণের ডান দিকটি একটি পরিবর্তনশীলের উপর নির্ভর করে এবং তাই, যদি এবং শুধুমাত্র ডান দিকটি একটি ফাংশন G(x) ≥ 0 হয় তবে একটি সমাধান আছে। মূল সমীকরণটি দুটি উপায়ে সমাধান করা যেতে পারে: 1 উপায়:স্ট্যান্ডার্ড, তার সংজ্ঞার উপর ভিত্তি করে মডিউলের প্রকাশের উপর ভিত্তি করে এবং দুটি সিস্টেমের সংমিশ্রণে একটি সমতুল্য রূপান্তর নিয়ে গঠিত। │ চ(x)│ =জি(এক্স)

G(x) ফাংশনের জন্য একটি জটিল রাশির ক্ষেত্রে এবং F(x) ফাংশনের জন্য একটি কম জটিল রাশির ক্ষেত্রে এই পদ্ধতিটি ব্যবহার করা যুক্তিসঙ্গত, যেহেতু এটি ফাংশন F(x) এর সাথে অসমতা সমাধান করার কথা। ২টি পথ:এটি একটি সমতুল্য সিস্টেমে রূপান্তর নিয়ে গঠিত যেখানে ডান দিকে একটি শর্ত আরোপ করা হয়। │ চ(এক্স)│= জি(এক্স)

এই পদ্ধতিটি ব্যবহার করা আরও সুবিধাজনক যদি G(x) ফাংশনের অভিব্যক্তিটি F(x) ফাংশনের তুলনায় কম জটিল হয়, যেহেতু অসমতা G(x) ≥ 0 এর সমাধান ধরে নেওয়া হয়। উপরন্তু, ক্ষেত্রে বেশ কয়েকটি মডিউলের মধ্যে, এই পদ্ধতিটি দ্বিতীয় বিকল্পটি ব্যবহার করার পরামর্শ দেওয়া হয়। উদাহরণ: №1. সমীকরণটি সমাধান করুন: │x + 2│= 6 -2x
(1 উপায়) উত্তরঃ x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(২টি পথ) উত্তরঃ শিকড়ের গুণফল ৩টি।
№3. সমীকরণটি সমাধান করুন, উত্তরে মূলের যোগফল লিখুন:
│x - 6 │ \u003d x 2 - 5x + 9

উত্তর: মূলের যোগফল 4।
অনুশীলন: №9. │x + 4│= - 3x №10. সমীকরণটি সমাধান করুন, উত্তরে সমাধানের সংখ্যা নির্দেশ করুন: │x 2 + x - 1 │ \u003d 2x - 1 №11 . সমীকরণটি সমাধান করুন, উত্তরে মূলের গুণফল নির্দেশ করুন: │x + 3 │ \u003d x 2 + x - 6

বিভাগ 4. ফর্মের সমীকরণ │F(x)│= F(x) এবং │F(x)│= - F(x)

এই ধরণের সমীকরণগুলিকে কখনও কখনও "সুন্দর" বলা হয়। যেহেতু সমীকরণের ডান দিকটি পরিবর্তনশীলের উপর নির্ভর করে, তাই সমাধান বিদ্যমান থাকে যদি এবং শুধুমাত্র যদি ডান দিকটি অ-নেতিবাচক হয়। অতএব, মূল সমীকরণগুলি অসমতার সমতুল্য:
│F(x)│= F(x) F(x) ≥ 0 এবং │F(x)│= - F(x) F(x) উদাহরণ: №1 . সমীকরণটি সমাধান করুন, উত্তরে ছোট পূর্ণসংখ্যার মূল নির্দেশ করুন: │5x - 3│ \u003d 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0.6 উত্তরঃ x = 1№2. সমীকরণটি সমাধান করুন, উত্তরে ব্যবধানের দৈর্ঘ্য নির্দেশ করুন: │x 2 - 9 │ \u003d 9 - x 2 x 2 - 9 ≤ 0 (x - 3) (x + 3) ≤ 0 [- 3; 3] উত্তর: ব্যবধানের দৈর্ঘ্য 6।№3 . সমীকরণটি সমাধান করুন, উত্তরে পূর্ণসংখ্যা সমাধানের সংখ্যা নির্দেশ করুন: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] উত্তর: 4টি সম্পূর্ণ সমাধান।№4 . সমীকরণটি সমাধান করুন, উত্তরে বৃহত্তম মূল নির্দেশ করুন:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 \u003d 0 D \u003d 5 x 1.2 \u003d
≈ 1,4

উত্তরঃ x = 3।

অনুশীলন: №12. সমীকরণটি সমাধান করুন, উত্তরে পুরো মূল নির্দেশ করুন: │x 2 + 6x + 8 │= x 2 + 6x + 8 №13. সমীকরণটি সমাধান করুন, উত্তরে পূর্ণসংখ্যা সমাধানের সংখ্যা নির্দেশ করুন: │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. সমীকরণটি সমাধান করুন, উত্তরে একটি পূর্ণসংখ্যা নির্দেশ করুন যা সমীকরণের মূল নয়:

বিভাগ 5. ফর্মের সমীকরণ │F(x)│= │G(x)│

যেহেতু সমীকরণের উভয় দিকই নেতিবাচক নয়, তাই সমাধান দুটি ক্ষেত্রে বিবেচনা করা জড়িত: সাবমডুলার এক্সপ্রেশন চিহ্নে সমান বা বিপরীত। অতএব, মূল সমীকরণটি দুটি সমীকরণের সমন্বয়ের সমতুল্য: │ চ(এক্স)│= │ জি(এক্স)│
উদাহরণ: №1. সমীকরণটি সমাধান করুন, উত্তরে পুরো মূল নির্দেশ করুন: │x + 3│ \u003d │2x - 1│
উত্তরঃ integer root x = 4.№2. সমীকরণটি সমাধান করুন: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
উত্তরঃ x = 2।№3 . সমীকরণটি সমাধান করুন, উত্তরে শিকড়ের গুণফল নির্দেশ করুন:




সমীকরণের মূল 4x 2 + 2x - 1 \u003d 0 x 1.2 \u003d - 1±√5 / 4 উত্তর: শিকড়ের গুণফল 0.25। অনুশীলন: №15 . সমীকরণটি সমাধান করুন, উত্তরে সম্পূর্ণ সমাধান নির্দেশ করুন: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. সমীকরণটি সমাধান করুন, উত্তরে ছোট মূল নির্দেশ করুন: │5x - 3│=│7 - x│ №17 . সমীকরণটি সমাধান করুন, উত্তরে মূলের যোগফল লিখুন:

অধ্যায় 6. অ-মানক সমীকরণ সমাধানের উদাহরণ

এই বিভাগে, আমরা অ-মানক সমীকরণগুলির উদাহরণ বিবেচনা করি, যার সমাধানে অভিব্যক্তির পরম মান সংজ্ঞা দ্বারা প্রকাশিত হয়। উদাহরণ:

№1. সমীকরণটি সমাধান করুন, উত্তরে মূলের যোগফল নির্দেশ করুন: x │x│- 5x - 6 \u003d 0
উত্তরঃ মূলের যোগফল 1 №2. . সমীকরণটি সমাধান করুন, উত্তরে ছোট মূল নির্দেশ করুন: x 2 - 4x
- 5 = 0
উত্তর: ছোট মূল x = - 5। №3. সমীকরণটি সমাধান করুন:

উত্তরঃ x = -1. অনুশীলন: №18. সমীকরণটি সমাধান করুন এবং মূলের যোগফল লিখুন: x │3x + 5│= 3x 2 + 4x + 3
№19. সমীকরণটি সমাধান করুন: x 2 - 3x \u003d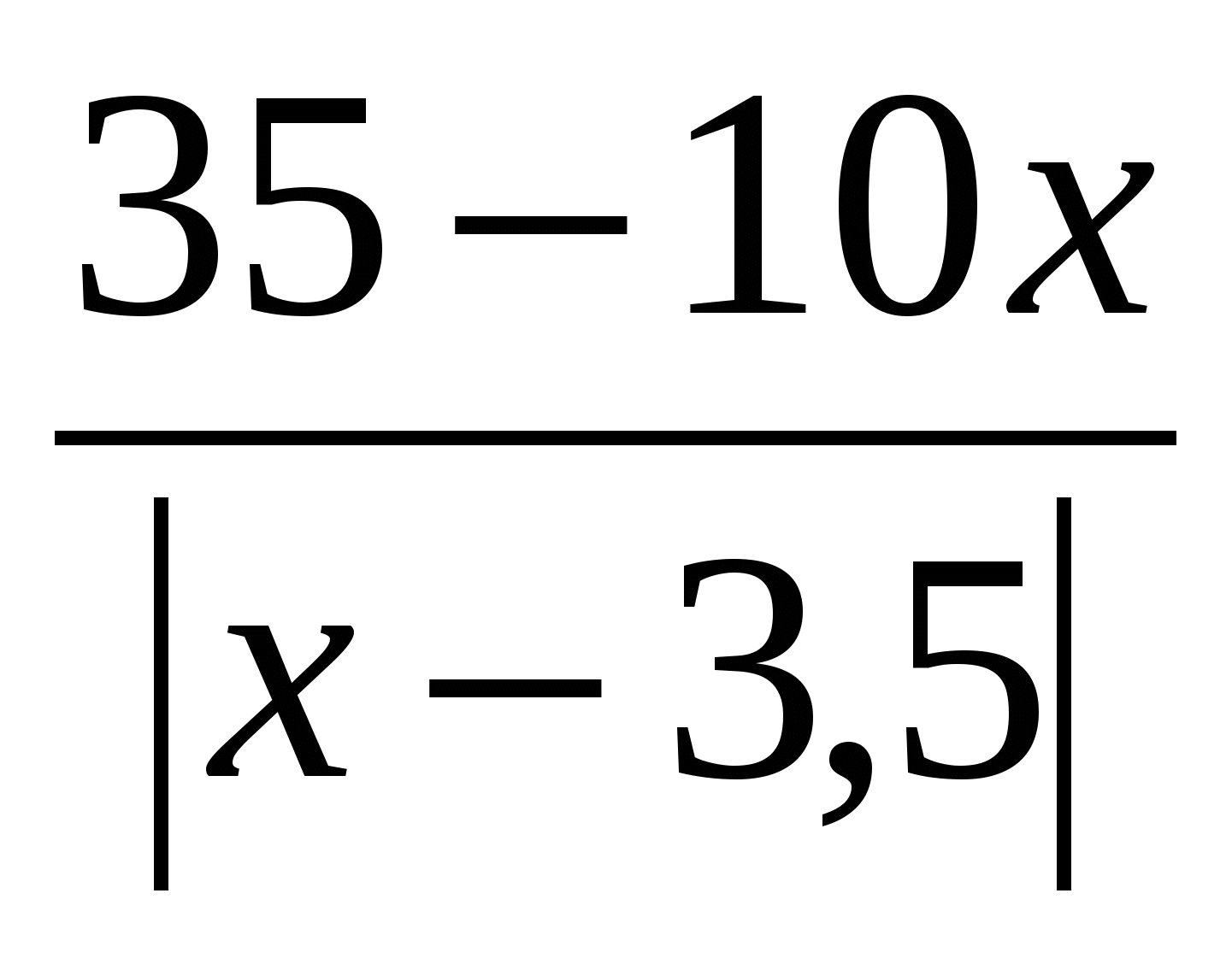

№20. সমীকরণটি সমাধান করুন:

বিভাগ 7. ফর্মের সমীকরণ │F(x)│+│G(x)│=0

এই ধরনের একটি সমীকরণের বাম দিকে, অ-ঋণাত্মক রাশির যোগফল দেখতে সহজ। অতএব, মূল সমীকরণের একটি সমাধান আছে যদি এবং শুধুমাত্র যদি উভয় পদ একই সাথে শূন্যের সমান হয়। সমীকরণটি সমীকরণের সিস্টেমের সমতুল্য: │ চ(এক্স)│+│ জি(এক্স)│=0
উদাহরণ: №1 . সমীকরণটি সমাধান করুন:
উত্তরঃ x = 2। №2. সমীকরণটি সমাধান করুন: উত্তরঃ x = 1। অনুশীলন: №21. সমীকরণটি সমাধান করুন: №22 . সমীকরণটি সমাধান করুন, উত্তরে মূলের যোগফল লিখুন: №23 . সমীকরণটি সমাধান করুন, উত্তরে সমাধানের সংখ্যা নির্দেশ করুন:

বিভাগ 8. ফর্মের সমীকরণ

এই ধরণের সমীকরণগুলি সমাধান করতে, বিরতির পদ্ধতি ব্যবহার করা হয়। যদি এটি মডিউলগুলির ক্রমিক সম্প্রসারণ দ্বারা সমাধান করা হয়, তাহলে আমরা পাই nসিস্টেমের সেট, যা খুবই কষ্টকর এবং অসুবিধাজনক। ব্যবধান পদ্ধতির অ্যালগরিদম বিবেচনা করুন: 1)। পরিবর্তনশীল মান খুঁজুন এক্স, যার জন্য প্রতিটি মডিউল শূন্যের সমান (সাবমডিউল এক্সপ্রেশনের শূন্য):
2)। প্রাপ্ত মানগুলি একটি সংখ্যা রেখায় চিহ্নিত করা হয়েছে, যা ব্যবধানে বিভক্ত (যথাক্রমে, ব্যবধানের সংখ্যা সমান n+1 3)। প্রতিটি প্রাপ্ত ব্যবধানে প্রতিটি মডিউল কী চিহ্ন দিয়ে প্রকাশ করা হয়েছে তা নির্ধারণ করুন (একটি সমাধান করার সময়, আপনি একটি সংখ্যা রেখা ব্যবহার করতে পারেন, এতে চিহ্নগুলি চিহ্নিত করে) 4)। মূল সমীকরণ সেটের সমতুল্য n+1 সিস্টেম, যার প্রতিটিতে ভেরিয়েবলের সদস্যতা নির্দেশিত হয় এক্সব্যবধানগুলির মধ্যে একটি। উদাহরণ: №1 . সমীকরণটি সমাধান করুন, উত্তরে বৃহত্তম মূল নির্দেশ করুন:
এক). সাবমডিউল এক্সপ্রেশনের শূন্য খুঁজে বের করা যাক: x = 2; x = -3 2)। আমরা সংখ্যা লাইনে পাওয়া মানগুলি চিহ্নিত করি এবং প্রাপ্ত ব্যবধানে প্রতিটি মডিউল কী চিহ্ন দিয়ে প্রকাশ করা হয়েছে তা নির্ধারণ করি:
x – 2 x – 2 x – 2 - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- কোন সমাধান নেই সমীকরণটির দুটি মূল রয়েছে। উত্তর: বৃহত্তম মূল হল x = 2। №2. সমীকরণটি সমাধান করুন, উত্তরে পুরো মূলটি লিখুন:
এক). সাবমডিউল এক্সপ্রেশনের শূন্য খুঁজে বের করা যাক: x = 1.5; x = - 1 2)। আমরা সংখ্যা লাইনে পাওয়া মানগুলি চিহ্নিত করি এবং প্রাপ্ত ব্যবধানে প্রতিটি মডিউল কী চিহ্ন দিয়ে প্রকাশ করা হয়েছে তা নির্ধারণ করি: x + 1 x + 1 x + 1 - + +
-1 1.5 х 2х – 3 2х – 3 2х – 3 - - +
3).
শেষ সিস্টেমের কোন সমাধান নেই, তাই, সমীকরণটির দুটি মূল রয়েছে। সমীকরণটি সমাধান করার সময়, আপনার দ্বিতীয় মডিউলের সামনে "-" চিহ্নটিতে মনোযোগ দেওয়া উচিত। উত্তরঃ integer root x = 7. №3. সমীকরণটি সমাধান করুন, উত্তরে মূলের যোগফল নির্দেশ করুন: 1)। সাবমডিউল এক্সপ্রেশনের শূন্য খুঁজে বের করা যাক: x = 5; x = 1; x = - 2 2)। আমরা সংখ্যা লাইনে পাওয়া মানগুলি চিহ্নিত করি এবং প্রাপ্ত ব্যবধানে প্রতিটি মডিউল কী চিহ্ন দিয়ে প্রকাশ করা হয়েছে তা নির্ধারণ করি: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
সমীকরণটির দুটি মূল x = 0 এবং 2 আছে। উত্তরঃ মূলের যোগফল 2। №4 . সমীকরণটি সমাধান করুন: 1)। সাবমডিউল এক্সপ্রেশনের শূন্য খুঁজে বের করা যাক: x = 1; x = 2; x = 3. 2)। আসুন প্রাপ্ত ব্যবধানে প্রতিটি মডিউল প্রসারিত করা হয় এমন চিহ্নটি নির্ধারণ করি। 3)।
আমরা প্রথম তিনটি সিস্টেমের সমাধান একত্রিত করি। উত্তর: ; x = 5।
অনুশীলন: №24. সমীকরণটি সমাধান করুন:
№25. সমীকরণটি সমাধান করুন, উত্তরে মূলের যোগফল লিখুন: №26. সমীকরণটি সমাধান করুন, উত্তরে ছোট মূল নির্দেশ করুন: №27. সমীকরণটি সমাধান করুন, আপনার উত্তরে বড় রুট দিন:

বিভাগ 9. একাধিক মডিউল সমন্বিত সমীকরণ

একাধিক মডিউল সমন্বিত সমীকরণগুলি সাবমডিউল এক্সপ্রেশনে পরম মান ধরে নেয়। এই ধরনের সমীকরণ সমাধানের মূল নীতি হল "বহিরাগত" থেকে শুরু করে মডিউলগুলির অনুক্রমিক প্রকাশ। সমাধানের সময়, সেকশন নং 1, নং 3 এ আলোচিত কৌশলগুলি ব্যবহার করা হয়েছে।

উদাহরণ: №1. সমীকরণটি সমাধান করুন:
উত্তরঃ x = 1; - এগারো №2. সমীকরণটি সমাধান করুন:
উত্তরঃ x = 0; 4; - 4। №3. সমীকরণটি সমাধান করুন, উত্তরে শিকড়ের গুণফল নির্দেশ করুন:
উত্তরঃ শিকড়ের গুণফল 8। №4. সমীকরণটি সমাধান করুন:
জনসংখ্যার সমীকরণগুলি বোঝাও (1) এবং (2) এবং ডিজাইনের সুবিধার জন্য তাদের প্রতিটির সমাধান আলাদাভাবে বিবেচনা করুন। যেহেতু উভয় সমীকরণে একাধিক মডিউল রয়েছে, তাই সিস্টেমের সেটে সমতুল্য রূপান্তর করা আরও সুবিধাজনক। (1)

(2)


উত্তর:
অনুশীলন: №36. সমীকরণটি সমাধান করুন, উত্তরে মূলের যোগফল নির্দেশ করুন: 5 │3x-5│ \u003d 25 x №37. সমীকরণটি সমাধান করুন, যদি একাধিক শিকড় থাকে, উত্তরে মূলের যোগফল নির্দেশ করুন: │x + 2│ x - 3x - 10 = 1 №38. সমীকরণটি সমাধান করুন: 3 │2x -4│ \u003d 9 │x│ №39. সমীকরণটি সমাধান করুন, উত্তরে এর জন্য শিকড়ের সংখ্যা নির্দেশ করুন: 2 │ sin x │ = √2 №40 . সমীকরণটি সমাধান করুন, উত্তরে শিকড়ের সংখ্যা নির্দেশ করুন:

বিভাগ 3. লগারিদমিক সমীকরণ।

নিম্নলিখিত সমীকরণগুলি সমাধান করার আগে, লগারিদমের বৈশিষ্ট্য এবং লগারিদমিক ফাংশন পর্যালোচনা করা প্রয়োজন। উদাহরণ: №1. সমীকরণটি সমাধান করুন, উত্তরে মূলের গুণফল নির্দেশ করুন: লগ 2 (x + 1) 2 + লগ 2 │x + 1 │ \u003d 6 O.D.Z। x+1≠0 x≠ - 1

কেস 1: যদি x ≥ - 1 হয়, তাহলে লগ 2 (x+1) 2 + লগ 2 (x+1) = 6 লগ 2 (x+1) 3 = লগ 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – শর্তটি সন্তুষ্ট করে x ≥ - 1 2 ক্ষেত্রে: যদি x লগ 2 (x+1) 2 + লগ 2 (-x-1) = 6 লগ 2 (x+1) 2 + লগ 2 (-(x+1)) = 6 লগ 2 (-(x+1) 3) = লগ 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – শর্ত পূরণ করে x - 1
উত্তরঃ শিকড়ের গুণফল 15টি।
№2. সমীকরণটি সমাধান করুন, উত্তরে মূলের যোগফল নির্দেশ করুন: lg
O.D.Z.

উত্তর: মূলের যোগফল 0.5।
№3. সমীকরণটি সমাধান করুন: লগ 5
O.D.Z.

উত্তরঃ x = 9। №4. সমীকরণটি সমাধান করুন: │2 + লগ 0.2 x│+ 3 = │1 + লগ 5 x│ O.D.Z. x > 0 অন্য বেসে যাওয়ার সূত্রটি ব্যবহার করা যাক। │2 - লগ 5 x│+ 3 = │1 + লগ 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 সাবমডিউল এক্সপ্রেশনের শূন্য বের করা যাক: x = 25; x \u003d এই সংখ্যাগুলি অনুমোদিত মানের ক্ষেত্রফলকে তিনটি ব্যবধানে ভাগ করে, তাই সমীকরণটি তিনটি সিস্টেমের সামগ্রিকতার সমতুল্য।
উত্তর: )