ফাংশন বলা হয় ব্যবধানে বাড়ছে
, যদি কোন পয়েন্টের জন্য

অসমতা
(বৃহত্তর মানআর্গুমেন্ট ফাংশনের বড় মানের সাথে মিলে যায়)।

একইভাবে, ফাংশন
ডাকা ব্যবধানে কমছে
, যদি কোন পয়েন্টের জন্য
শর্তের অধীনে এই ব্যবধান থেকে
অসমতা
(আর্গুমেন্টের একটি বড় মান ফাংশনের একটি ছোট মানের সাথে মিলে যায়)।

ব্যবধানে বাড়ছে
এবং ব্যবধানে কমছে
ফাংশন বলা হয় ব্যবধানে একঘেয়েমি
.

একটি পার্থক্যযোগ্য ফাংশনের ডেরিভেটিভ জানা আমাদেরকে এর একঘেয়েতার ব্যবধান খুঁজে পেতে দেয়।

উপপাদ্য (ফাংশন বাড়ানোর জন্য যথেষ্ট শর্ত)।
ফাংশন
ব্যবধানে ইতিবাচক
, তারপর ফাংশন
এই ব্যবধানে একঘেয়ে বেড়ে যায়।

উপপাদ্য (ফাংশন হ্রাস করার জন্য যথেষ্ট শর্ত)।ডেরিভেটিভ যদি ব্যবধানে পার্থক্যযোগ্য হয়
ফাংশন
ব্যবধানে নেতিবাচক
, তারপর ফাংশন
এই ব্যবধানে একঘেয়ে কমে যায়।

জ্যামিতিক ইন্দ্রিয় এই উপপাদ্যগুলির মধ্যে হ'ল হ্রাসকৃত ফাংশনের ব্যবধানে, ফাংশনগুলি অক্ষের সাথে গ্রাফের স্পর্শক গঠন করে
স্থূল কোণ, এবং বৃদ্ধির বিরতিতে - তীক্ষ্ণ (চিত্র 1 দেখুন)।

উপপাদ্য (একটি ফাংশনের একঘেয়েতার জন্য প্রয়োজনীয় শর্ত)।যদি ফাংশন
পার্থক্যযোগ্য এবং
(
) ব্যবধানে
, তাহলে এই ব্যবধানে এটি হ্রাস পায় না (বাড়ে না)।

একটি ফাংশনের একঘেয়েতার ব্যবধান খুঁজে বের করার জন্য অ্যালগরিদম
:

উদাহরণ।একটি ফাংশনের একঘেয়েমি ব্যবধান খুঁজুন
.

ডট ডাকা ফাংশনের সর্বোচ্চ পয়েন্ট

যেমন সবার জন্য , শর্ত সন্তুষ্ট
, অসমতা
.

সর্বাধিক ফাংশন সর্বাধিক বিন্দুতে ফাংশনের মান।

চিত্র 2 একটি ফাংশনের গ্রাফের একটি উদাহরণ দেখায় যার পয়েন্টে ম্যাক্সিমা রয়েছে
.

ডট ডাকা ফাংশনের সর্বনিম্ন পয়েন্ট
যদি কিছু নম্বর থাকে
যেমন সবার জন্য , শর্ত সন্তুষ্ট
, অসমতা
. ডুমুর 2 ফাংশন একটি বিন্দুতে একটি সর্বনিম্ন আছে .

উচ্চ এবং নিচু জন্য একটি সাধারণ নাম আছে - চরম . তদনুসারে, সর্বোচ্চ এবং সর্বনিম্ন পয়েন্ট বলা হয় চরম পয়েন্ট .

একটি সেগমেন্টে সংজ্ঞায়িত একটি ফাংশন শুধুমাত্র এই বিভাগের ভিতরের পয়েন্টগুলিতে সর্বাধিক এবং সর্বনিম্ন থাকতে পারে। একটি সেগমেন্টের সর্বোচ্চ এবং সর্বনিম্ন মানের সাথে একটি ফাংশনের সর্বাধিক এবং সর্বনিম্ন মানকে বিভ্রান্ত করাও অসম্ভব - এগুলি মৌলিকভাবে ভিন্ন ধারণা।

চরম পয়েন্টে, ডেরিভেটিভের বিশেষ বৈশিষ্ট্য রয়েছে।

উপপাদ্য (একটি চরমের জন্য প্রয়োজনীয় শর্ত)।বিন্দুতে যাক ফাংশন
একটি extremum আছে. তারপর হয়
বিদ্যমান নেই, বা
.

ফাংশন ডোমেইন থেকে যারা পয়েন্ট, যা
বিদ্যমান নেই বা যার মধ্যে
, ডাকল ফাংশনের সমালোচনামূলক পয়েন্ট .

সুতরাং, চরম পয়েন্টগুলি সমালোচনামূলক পয়েন্টগুলির মধ্যে রয়েছে। সাধারণ ক্ষেত্রে, সমালোচনামূলক বিন্দু একটি চরম বিন্দু হতে হবে না. যদি কোনো সময়ে কোনো ফাংশনের ডেরিভেটিভ শূন্যের সমান হয়, তাহলে এর মানে এই নয় যে এই সময়ে ফাংশনের একটি এক্সট্রিম আছে।

উদাহরণ।বিবেচনা
. আমাদের আছে
, কিন্তু বিন্দু
একটি চরম বিন্দু নয় (চিত্র 3 দেখুন)।

উপপাদ্য (একটি চরমের জন্য প্রথম পর্যাপ্ত শর্ত)।বিন্দুতে যাক ফাংশন
একটানা, এবং ডেরিভেটিভ
একটি বিন্দুর মধ্য দিয়ে যাওয়ার সময় পরিবর্তন চিহ্ন। তারপর – চরম বিন্দু: সর্বোচ্চ, যদি চিহ্নটি “+” থেকে “–” তে পরিবর্তিত হয় এবং সর্বনিম্ন, যদি “–” থেকে “+” হয়।

যদি, একটি বিন্দুর মধ্য দিয়ে যাওয়ার সময় ডেরিভেটিভ চিহ্ন পরিবর্তন করে না, তারপর বিন্দুতে কোন চরম আছে.

উপপাদ্য (একটি চরমের জন্য দ্বিতীয় পর্যাপ্ত শর্ত)।বিন্দুতে যাক একটি দ্বিগুণ পার্থক্যযোগ্য ফাংশনের ডেরিভেটিভ
শূন্যের সমান (
), এবং এই সময়ে এর দ্বিতীয় ডেরিভেটিভ হল অশূন্য (
) এবং বিন্দুর কিছু আশেপাশে অবিচ্ছিন্ন . তারপর - চরম বিন্দু
; এ
সর্বনিম্ন পয়েন্ট, এবং
এই সর্বোচ্চ পয়েন্ট.

প্রথম পর্যাপ্ত এক্সট্রিম কন্ডিশন ব্যবহার করে ফাংশনের এক্সট্রিমাম খুঁজে বের করার জন্য অ্যালগরিদম:

ডেরিভেটিভ খুঁজুন.

ফাংশনের সমালোচনামূলক পয়েন্ট খুঁজুন।

প্রতিটি সমালোচনামূলক বিন্দুর বাম এবং ডানে ডেরিভেটিভের চিহ্নটি পরীক্ষা করুন এবং চরমের উপস্থিতি সম্পর্কে একটি উপসংহার আঁকুন।

ফাংশনের চরম মান খুঁজুন।

দ্বিতীয় পর্যাপ্ত চরম অবস্থা ব্যবহার করে একটি ফাংশনের এক্সট্রিমা খোঁজার জন্য অ্যালগরিদম:

উদাহরণ।একটি ফাংশনের চরমতা খুঁজুন
.

একটি ফাংশনের বৃদ্ধি, হ্রাস এবং চরম

একটি ফাংশনের বৃদ্ধি, হ্রাস এবং চরমের ব্যবধান খুঁজে বের করার মতো স্বাধীন কাজ, এবং অন্যান্য কাজের সবচেয়ে গুরুত্বপূর্ণ অংশ, বিশেষ করে, সম্পূর্ণ ফাংশন অধ্যয়ন. প্রাথমিক তথ্যফাংশন বৃদ্ধি, হ্রাস এবং চরম সম্পর্কে দেওয়া হয় ডেরিভেটিভের উপর তাত্ত্বিক অধ্যায়, যা আমি প্রাথমিক অধ্যয়নের জন্য অত্যন্ত সুপারিশ করছি (বা পুনরাবৃত্তি)- এছাড়াও কারণে যে নিম্নলিখিত উপাদান খুব উপর ভিত্তি করে ডেরিভেটিভ এর সারমর্মএই নিবন্ধের একটি সুরেলা ধারাবাহিকতা হচ্ছে. যদিও, যদি সময় ফুরিয়ে যায়, তাহলে আজকের পাঠের উদাহরণ থেকে একটি সম্পূর্ণ আনুষ্ঠানিক কাজও সম্ভব।

এবং আজ বাতাসে বিরল ঐক্যের চেতনা, এবং আমি সরাসরি অনুভব করতে পারি যে উপস্থিত সকলেই কামনায় জ্বলছে ডেরিভেটিভ ব্যবহার করে একটি ফাংশন অন্বেষণ করতে শিখুন. অতএব, যুক্তিসঙ্গত ভাল চিরন্তন পরিভাষা অবিলম্বে আপনার মনিটর পর্দায় প্রদর্শিত হবে.

কিসের জন্য? সবচেয়ে ব্যবহারিক কারণগুলির মধ্যে একটি হল: একটি নির্দিষ্ট কাজের জন্য সাধারণত আপনার কী প্রয়োজন তা স্পষ্ট করতে!

ফাংশন একঘেয়েমি। এক্সট্রিমাম পয়েন্ট এবং ফাংশন এক্সট্রিমা

কিছু ফাংশন বিবেচনা করা যাক. সরলভাবে, আমরা যে অনুমান একটানাসম্পূর্ণ নম্বর লাইনে:

ঠিক সেই ক্ষেত্রে, আমরা অবিলম্বে সম্ভাব্য বিভ্রম থেকে মুক্তি পাব, বিশেষ করে সেই পাঠকদের জন্য যারা সম্প্রতি পরিচিত হয়েছেন ফাংশনের চিহ্ন স্থিরতার ব্যবধান. এখন আমাদের আগ্রহী নই, কিভাবে ফাংশনের গ্রাফটি অক্ষের সাপেক্ষে অবস্থিত (উপরে, নীচে, যেখানে এটি অক্ষ অতিক্রম করে)। প্ররোচিত করার জন্য, মানসিকভাবে অক্ষগুলি মুছে ফেলুন এবং একটি গ্রাফ ছেড়ে দিন। কারণ এর মধ্যেই স্বার্থ রয়েছে।

ফাংশন বৃদ্ধি পায়একটি ব্যবধানে যদি সম্পর্ক দ্বারা সম্পর্কিত এই ব্যবধানের যেকোনো দুটি পয়েন্টের জন্য, অসমতা সত্য। অর্থাৎ, আর্গুমেন্টের একটি বৃহত্তর মান ফাংশনের একটি বৃহত্তর মানের সাথে মিলে যায় এবং এর গ্রাফটি "নীচ থেকে উপরে" যায়। ডেমো ফাংশন ব্যবধানে বৃদ্ধি পায়।

একইভাবে, ফাংশন হ্রাসএকটি ব্যবধানে যদি প্রদত্ত ব্যবধানের যেকোনো দুটি বিন্দুর জন্য, যেমন, অসমতা সত্য। অর্থাৎ, আর্গুমেন্টের একটি বড় মান ফাংশনের একটি ছোট মানের সাথে মিলে যায় এবং এর গ্রাফটি "উপর থেকে নীচে" যায়। ব্যবধানে আমাদের ফাংশন কমে যাচ্ছে .

যদি একটি ফাংশন একটি ব্যবধানে বৃদ্ধি বা হ্রাস পায়, তবে তাকে বলা হয় কঠোরভাবে একঘেয়েএই ব্যবধানে একঘেয়েমি কি? আক্ষরিক অর্থে নিন - একঘেয়েমি।

এটি সংজ্ঞায়িত করাও সম্ভব অ-হ্রাসফাংশন (প্রথম সংজ্ঞায় শিথিল অবস্থা) এবং অ বৃদ্ধিফাংশন (২য় সংজ্ঞায় নরম অবস্থা)। একটি ব্যবধানে একটি অ-হ্রাস বা বৃদ্ধি না হওয়া ফাংশনকে একটি নির্দিষ্ট ব্যবধানে একঘেয়ে ফাংশন বলা হয় (কঠোর একঘেয়েমি হল "শুধু" একঘেয়েতার একটি বিশেষ ক্ষেত্রে).

তত্ত্বটি অর্ধ-ব্যবধান, সেগমেন্ট সহ একটি ফাংশনের বৃদ্ধি / হ্রাস নির্ধারণের জন্য অন্যান্য পদ্ধতিগুলিও বিবেচনা করে, তবে আপনার মাথায় তেল-তেল-তেল ঢেলে না দেওয়ার জন্য, আমরা শ্রেণীবদ্ধ সংজ্ঞা সহ খোলা ব্যবধানে কাজ করতে সম্মত - এটি আরও পরিষ্কার, এবং অনেকগুলি ব্যবহারিক সমস্যা সমাধানের জন্য যথেষ্ট।

এইভাবে, আমার নিবন্ধগুলিতে, "একটি ফাংশনের একঘেয়েতা" শব্দটি প্রায় সর্বদা লুকিয়ে থাকবে বিরতিকঠোর একঘেয়েমি(ফাংশনের কঠোর বৃদ্ধি বা কঠোর হ্রাস)।

পয়েন্ট পাড়া। শব্দের পরে ছাত্ররা যেখানে পারে সেখানে ছড়িয়ে পড়ে এবং কোণে আতঙ্কে লুকিয়ে থাকে। …যদিও পোস্টের পর কচি সীমাতারা সম্ভবত আর লুকিয়ে রাখে না, তবে কেবল সামান্যই কাঁপছে =) চিন্তা করবেন না, এখন গাণিতিক বিশ্লেষণের উপপাদ্যগুলির কোনও প্রমাণ থাকবে না - আমার আরও কঠোরভাবে সংজ্ঞা প্রণয়নের জন্য প্রতিবেশীর প্রয়োজন ছিল চরম পয়েন্ট. আমরা স্মরণ করি:

আশেপাশের পয়েন্টপ্রদত্ত বিন্দু ধারণ করে ব্যবধানের নাম দিন, যখন সুবিধার জন্য ব্যবধানটিকে প্রায়শই প্রতিসম বলে ধরে নেওয়া হয়। উদাহরণস্বরূপ, একটি বিন্দু এবং এর আদর্শ প্রতিবেশী:

মূলত সংজ্ঞা:

বিন্দু বলা হয় কঠোর সর্বোচ্চ পয়েন্ট, যদি বিদ্যমানতার পাড়া, সবার জন্যযার মান, বিন্দু নিজেই ব্যতীত, অসমতা পূর্ণ হয়। আমাদের মাঝে নির্দিষ্ট উদাহরণএটি একটি বিন্দু।

বিন্দু বলা হয় কঠোর সর্বনিম্ন পয়েন্ট, যদি বিদ্যমানতার পাড়া, সবার জন্যযার মান, বিন্দু নিজেই ব্যতীত, অসমতা পূর্ণ হয়। অঙ্কনে - পয়েন্ট "এ"।

বিঃদ্রঃ : আশেপাশের প্রতিসাম্যের প্রয়োজনটি মোটেই প্রয়োজনীয় নয়৷ উপরন্তু, এটা গুরুত্বপূর্ণ অস্তিত্বের খুব বাস্তবতাআশেপাশের এলাকা (যদিও ক্ষুদ্র, এমনকি আণুবীক্ষণিক) যা নির্দিষ্ট শর্তগুলিকে সন্তুষ্ট করে

বিন্দু বলা হয় কঠোর চরম বিন্দুবা সহজভাবে চরম পয়েন্টফাংশন অর্থাৎ, এটি সর্বাধিক পয়েন্ট এবং সর্বনিম্ন পয়েন্টের জন্য একটি সাধারণ শব্দ।

"চরম" শব্দটি কীভাবে বুঝবেন? হ্যাঁ, যেমন সরাসরি একঘেয়েমি। রোলার কোস্টারের চরম পয়েন্ট।

একঘেয়েমির ক্ষেত্রে যেমন, তত্ত্বের মধ্যে রয়েছে এবং আরও সাধারণ অ-কঠোর পোস্টুলেট রয়েছে (যার অধীনে, অবশ্যই, বিবেচিত কঠোর মামলা পড়ে!):

বিন্দু বলা হয় সর্বোচ্চ পয়েন্ট, যদি বিদ্যমানএর চারপাশ, যেমন সবার জন্য
বিন্দু বলা হয় সর্বনিম্ন পয়েন্ট, যদি বিদ্যমানএর চারপাশ, যেমন সবার জন্যএই পাড়ার মূল্যবোধ, বৈষম্য ধরে রেখেছে।

মনে রাখবেন যে শেষ দুটি সংজ্ঞা অনুসারে, একটি ধ্রুবক ফাংশনের যেকোনো বিন্দু (বা কিছু ফাংশনের একটি "সমতল এলাকা") সর্বোচ্চ বিন্দু এবং একটি সর্বনিম্ন বিন্দু উভয়ই বিবেচনা করা হয়! ফাংশন, যাইহোক, উভয়ই অ-বর্ধমান এবং অ-হ্রাস, অর্থাৎ একঘেয়ে। যাইহোক, আমরা এই যুক্তিগুলি তাত্ত্বিকদের উপর ছেড়ে দিয়েছি, যেহেতু অনুশীলনে আমরা প্রায় সবসময়ই ঐতিহ্যগত "পাহাড়" এবং "হোলো" (অঙ্কন দেখুন) একটি অনন্য "পাহাড়ের রাজা" বা "মার্শ রাজকুমারী" নিয়ে চিন্তা করি। বিভিন্ন হিসাবে, এটি ঘটে বিন্দু, উপরে বা নিচে নির্দেশিত, উদাহরণস্বরূপ, বিন্দুতে ফাংশনের ন্যূনতম।

ওহ, উপায় দ্বারা, ওহ রয়্যালটি:
- অর্থ বলা হয় সর্বোচ্চফাংশন
- অর্থ বলা হয় সর্বনিম্নফাংশন

সাধারণ নাম - চরমফাংশন

আপনার কথার সাথে সতর্ক থাকুন!

চরম পয়েন্ট"x" মান।
চরম- "গেম" মান।

! বিঃদ্রঃ : কখনও কখনও তালিকাভুক্ত পদগুলি "x-y" পয়েন্টগুলিকে নির্দেশ করে যা সরাসরি ফাংশনের গ্রাফে থাকে৷

একটি ফাংশন কয়টি এক্সট্রিমা থাকতে পারে?

কোনটিই নয়, 1, 2, 3, … ইত্যাদি অসীমে. উদাহরণস্বরূপ, সাইনের সর্বনিম্ন এবং সর্বোচ্চের অসীম সংখ্যা রয়েছে।

গুরুত্বপূর্ণ!শব্দ "সর্বোচ্চ ফাংশন" অভিন্ন নয়শব্দ "একটি ফাংশনের সর্বোচ্চ মান"। এটা দেখা সহজ যে মান শুধুমাত্র স্থানীয় আশেপাশে সর্বাধিক, এবং উপরের বাম দিকে "আরো আকস্মিকভাবে কমরেড" আছে। একইভাবে, "ন্যূনতম ফাংশন" "ন্যূনতম ফাংশন মান" এর মতো নয় এবং অঙ্কনে আমরা দেখতে পাচ্ছি যে মানটি শুধুমাত্র একটি নির্দিষ্ট এলাকায় সর্বনিম্ন। এই বিষয়ে, চরম পয়েন্ট বলা হয় স্থানীয় চরম পয়েন্ট, এবং চরম স্থানীয় চরম. তারা হাঁটতে হাঁটতে ঘুরে বেড়ায় এবং বিশ্বব্যাপীভাই সুতরাং, যে কোনো প্যারাবোলার শীর্ষবিন্দুতে থাকে বিশ্বব্যাপী সর্বনিম্নবা বিশ্বব্যাপী সর্বোচ্চ. আরও, আমি চরম প্রকারের মধ্যে পার্থক্য করব না, এবং ব্যাখ্যাটি সাধারণ শিক্ষাগত উদ্দেশ্যে আরও উচ্চারিত হয় - অতিরিক্ত বিশেষণ "স্থানীয়" / "বিশ্ব" অবাক করে নেওয়া উচিত নয়।

আসুন একটি কন্ট্রোল শট দিয়ে তত্ত্বে আমাদের সংক্ষিপ্ত ডিগ্রেশনের সংক্ষিপ্তসার করা যাক: কাজটি "একঘেয়েমির ব্যবধান এবং একটি ফাংশনের চরম বিন্দু খুঁজে বের করার" অর্থ কী?

সূত্র খুঁজে পেতে অনুরোধ করে:

- ফাংশনের বৃদ্ধি / হ্রাসের ব্যবধান (অ-হ্রাস, অ-বাড়ন্ত অনেক কম দেখা যায়);

- সর্বোচ্চ পয়েন্ট এবং/অথবা সর্বনিম্ন পয়েন্ট (যদি থাকে)। ঠিক আছে, ব্যর্থতা থেকে মিনিমা / ম্যাক্সিমা খুঁজে বের করা ভাল ;-)

এই সব সংজ্ঞায়িত কিভাবে?একটি ডেরিভেটিভ ফাংশনের সাহায্যে!

বৃদ্ধি, হ্রাসের ব্যবধানগুলি কীভাবে সন্ধান করবেন,
extremum পয়েন্ট এবং ফাংশনের extremums?

অনেক নিয়ম, আসলে, ইতিমধ্যে পরিচিত এবং থেকে বোঝা যায় ডেরিভেটিভের অর্থ সম্পর্কে পাঠ.

স্পর্শক ডেরিভেটিভ সুসংবাদ বহন করে যে ফাংশন জুড়ে বাড়ছে ডোমেইন.

কোট্যাঞ্জেন্ট এবং এর ডেরিভেটিভ সহ পরিস্থিতি ঠিক বিপরীত।

আর্কসিন ব্যবধানে বৃদ্ধি পায় - ডেরিভেটিভ এখানে ইতিবাচক: .
এর জন্য, ফাংশনটি সংজ্ঞায়িত কিন্তু পার্থক্যযোগ্য নয়। যাইহোক, ক্রিটিক্যাল পয়েন্টে একটি ডান-হাত ডেরিভেটিভ এবং একটি ডান-হাতের স্পর্শক এবং অন্য প্রান্তে, তাদের বাম-হাতের প্রতিরূপ রয়েছে।

আমি মনে করি আপনার জন্য আর্ক কোসাইন এবং এর ডেরিভেটিভের জন্য অনুরূপ যুক্তি বহন করা কঠিন হবে না।

এসব মামলার অনেকগুলোই রয়েছে ট্যাবুলার ডেরিভেটিভস, আমি আপনাকে মনে করিয়ে দিচ্ছি, সরাসরি থেকে অনুসরণ করুন ডেরিভেটিভের সংজ্ঞা.

কেন একটি ডেরিভেটিভ সঙ্গে একটি ফাংশন অন্বেষণ?

এই ফাংশনের গ্রাফটি দেখতে কেমন তা সম্পর্কে আরও ভাল ধারণা পেতে: যেখানে এটি "নিচে উপরে" যায়, যেখানে এটি "উপরের নিচে" যায়, যেখানে এটি উচ্চতার নিম্নে পৌঁছায় (যদি থাকে)। সমস্ত ফাংশন এত সহজ নয় - বেশিরভাগ ক্ষেত্রে, একটি নির্দিষ্ট ফাংশনের গ্রাফ সম্পর্কে আমাদের কোনও ধারণা নেই।

এটি আরও অর্থপূর্ণ উদাহরণের দিকে এগিয়ে যাওয়ার এবং বিবেচনা করার সময় একটি ফাংশনের একঘেয়েতা এবং চরমতার ব্যবধান খুঁজে বের করার জন্য অ্যালগরিদম:

উদাহরণ 1

একটি ফাংশনের ক্রমবর্ধমান/হ্রাসিত ব্যবধান এবং চরমতা খুঁজুন

সমাধান:

1) প্রথম ধাপ হল খুঁজে বের করা ফাংশন সুযোগ, এবং ব্রেকপয়েন্টগুলিও নোট করুন (যদি তারা বিদ্যমান থাকে)। এই ক্ষেত্রে, ফাংশনটি সম্পূর্ণ বাস্তব লাইনে অবিচ্ছিন্ন, এবং এই ক্রিয়াটি কিছুটা আনুষ্ঠানিক। কিন্তু কিছু ক্ষেত্রে, গুরুতর আবেগ এখানে ছড়িয়ে পড়ে, তাই আসুন অবহেলা না করে অনুচ্ছেদটি ব্যবহার করি।

2) অ্যালগরিদম দ্বিতীয় বিন্দু কারণে

একটি চরমের জন্য প্রয়োজনীয় শর্ত:

যদি বিন্দুতে একটি এক্সট্রিম্যাম থাকে, তাহলে হয় মানটি বিদ্যমান থাকে না.

সমাপ্তি দ্বারা বিভ্রান্ত? "মডুলো এক্স" ফাংশনের এক্সট্রিম .

শর্ত আবশ্যক, কিন্তু যথেষ্ট না, এবং কথোপকথন সবসময় সত্য হয় না. সুতরাং, এটি এখনও সমতা থেকে অনুসরণ করে না যে বিন্দুতে ফাংশনটি সর্বাধিক বা সর্বনিম্ন পৌঁছায়। একটি ক্লাসিক উদাহরণ ইতিমধ্যে উপরে আলোকিত হয়েছে - এটি একটি ঘনক প্যারাবোলা এবং এর সমালোচনামূলক বিন্দু।

তবে তা যেমনই হোক, প্রয়োজনীয় শর্তচরম সন্দেহজনক পয়েন্ট খুঁজে বের করার প্রয়োজন নির্দেশ করে। এটি করার জন্য, ডেরিভেটিভটি সন্ধান করুন এবং সমীকরণটি সমাধান করুন:

প্রথম নিবন্ধের শুরুতে ফাংশন গ্রাফ সম্পর্কেআমি আপনাকে বলেছিলাম কিভাবে একটি উদাহরণ ব্যবহার করে দ্রুত একটি প্যারাবোলা তৈরি করতে হয় : "... আমরা প্রথম ডেরিভেটিভটি গ্রহণ করি এবং এটিকে শূন্যে সমান করি: ... সুতরাং, আমাদের সমীকরণের সমাধান: - এই সময়ে প্যারাবোলার শীর্ষটি অবস্থিত ..."। এখন, আমি মনে করি সবাই বুঝতে পারছে কেন প্যারাবোলার শীর্ষটি ঠিক এই বিন্দুতে =) সাধারণভাবে, আমাদের এখানে অনুরূপ উদাহরণ দিয়ে শুরু করা উচিত, তবে এটি খুব সহজ (এমনকি একটি চাপাতার জন্যও)। উপরন্তু, সম্পর্কে পাঠের একেবারে শেষে একটি অ্যানালগ আছে ডেরিভেটিভ ফাংশন. তাহলে চলুন মাত্রা বাড়াই:

উদাহরণ 2

একঘেয়েমি ব্যবধান এবং একটি ফাংশনের চরমতা খুঁজুন

এটি একটি করণীয় উদাহরণ। পাঠের শেষে সমস্যার একটি সম্পূর্ণ সমাধান এবং একটি আনুমানিক সমাপ্তির নমুনা।

ভগ্নাংশ যুক্তিযুক্ত ফাংশন সহ সভার দীর্ঘ প্রতীক্ষিত মুহূর্ত এসেছে:

উদাহরণ 3

প্রথম ডেরিভেটিভ ব্যবহার করে একটি ফাংশন অন্বেষণ করুন

কীভাবে এক এবং একই কাজকে বিভিন্নভাবে সংস্কার করা যায় সেদিকে মনোযোগ দিন।

সমাধান:

1) ফাংশন বিন্দুতে অসীম বিরতি ভোগ করে।

2) আমরা সমালোচনামূলক পয়েন্ট সনাক্ত করি। আসুন প্রথম ডেরিভেটিভটি খুঁজে বের করি এবং এটিকে শূন্যের সাথে সমান করি:

আসুন সমীকরণটি সমাধান করি। একটি ভগ্নাংশ শূন্য হয় যখন এর লব শূন্য হয়:

সুতরাং, আমরা তিনটি গুরুত্বপূর্ণ পয়েন্ট পাই:

3) নম্বর লাইনের সমস্ত শনাক্ত করা বিন্দু আলাদা করে রাখুন এবং ব্যবধান পদ্ধতিডেরিভেটিভের লক্ষণগুলি সংজ্ঞায়িত করুন:

আমি আপনাকে মনে করিয়ে দিচ্ছি যে আপনাকে ব্যবধানের কিছু পয়েন্ট নিতে হবে, এতে ডেরিভেটিভের মান গণনা করুন এবং তার চিহ্ন নির্ধারণ করুন। এমনকি গণনা না করা, কিন্তু মৌখিকভাবে "অনুমান" করা আরও লাভজনক। উদাহরণস্বরূপ, ব্যবধানের সাথে সম্পর্কিত একটি বিন্দু নিন এবং প্রতিস্থাপনটি সম্পাদন করুন: .

দুটি "প্লাস" এবং একটি "বিয়োগ" একটি "বিয়োগ" দেয়, অতএব, যার অর্থ হল পুরো ব্যবধানে ডেরিভেটিভ নেতিবাচক।

ক্রিয়াটি, যেমন আপনি বোঝেন, ছয়টি ব্যবধানের প্রতিটির জন্য অবশ্যই করা উচিত। যাইহোক, মনে রাখবেন যে লব ফ্যাক্টর এবং হর যে কোনও ব্যবধানের যে কোনও বিন্দুর জন্য কঠোরভাবে ইতিবাচক, যা কাজটিকে ব্যাপকভাবে সরল করে।

সুতরাং, ডেরিভেটিভ আমাদের বলেছে যে ফাংশন নিজেই বৃদ্ধি পায় এবং দ্বারা হ্রাস পায়। ইউনিয়ন আইকনের সাথে একই ধরণের ব্যবধান বেঁধে রাখা সুবিধাজনক।

বিন্দুতে ফাংশনটি সর্বোচ্চ পৌঁছে যায়:
বিন্দুতে ফাংশনটি তার সর্বনিম্ন পৌঁছায়:

আপনি কেন দ্বিতীয় মান পুনরায় গণনা করতে পারবেন না সে সম্পর্কে চিন্তা করুন ;-)

একটি বিন্দুর মধ্য দিয়ে যাওয়ার সময়, ডেরিভেটিভ চিহ্ন পরিবর্তন করে না, তাই সেখানে ফাংশনটির কোন চরম নেই - এটি উভয়ই হ্রাস পেয়েছে এবং হ্রাস পাচ্ছে।

! এর পুনরাবৃত্তি করা যাক গুরুত্বপূর্ণ পয়েন্ট : পয়েন্টগুলিকে সমালোচনামূলক বলে মনে করা হয় না - তাদের একটি ফাংশন আছে নির্ধারিত না. সেই অনুযায়ী, এখানে চরমপন্থা নীতিগতভাবে হতে পারে না(যদিও ডেরিভেটিভ পরিবর্তন চিহ্ন)।

উত্তর: ফাংশন বৃদ্ধি পায় এবং কমে যায় বিন্দুতে ফাংশনের সর্বোচ্চ সীমায় পৌঁছে যায়: , এবং বিন্দুতে - সর্বনিম্ন: .

একঘেয়েমি ব্যবধান এবং চরমের জ্ঞান, প্রতিষ্ঠিত সঙ্গে মিলিত উপসর্গএকটি খুব ভাল ধারণা দেয় চেহারাফাংশন গ্রাফ। একজন গড় ব্যক্তি মৌখিকভাবে নির্ধারণ করতে সক্ষম যে একটি ফাংশন গ্রাফে দুটি উল্লম্ব অ্যাসিম্পটোট এবং একটি তির্যক অ্যাসিম্পটোট রয়েছে। এখানে আমাদের নায়ক:

এই ফাংশনের গ্রাফের সাথে অধ্যয়নের ফলাফলগুলিকে সংযুক্ত করার জন্য আবার চেষ্টা করুন।
সমালোচনামূলক পয়েন্টে কোন চরমপন্থা নেই, কিন্তু আছে বক্ররেখা মোচন(যা, একটি নিয়ম হিসাবে, অনুরূপ ক্ষেত্রে ঘটে)।

উদাহরণ 4

একটি ফাংশনের চরমতা খুঁজুন

উদাহরণ 5

একটি ফাংশনের একঘেয়েমি ব্যবধান, ম্যাক্সিমা এবং মিনিমা খুঁজুন

... শুধু এক ধরনের এক্স-ইন-এ-কিউব হলিডে আজ চালু হচ্ছে...
Soooo, গ্যালারিতে কে এই জন্য পান করার প্রস্তাব? =)

প্রতিটি কাজের নিজস্ব মৌলিক সূক্ষ্মতা এবং প্রযুক্তিগত সূক্ষ্মতা রয়েছে, যা পাঠের শেষে মন্তব্য করা হয়েছে।

একটি ফাংশনের প্রকৃতি নির্ধারণ করতে এবং তার আচরণ সম্পর্কে কথা বলতে, বৃদ্ধি এবং হ্রাসের ব্যবধান খুঁজে বের করা প্রয়োজন। এই প্রক্রিয়াটিকে ফাংশন এক্সপ্লোরেশন এবং প্লটিং বলা হয়। ফাংশনের বৃহত্তম এবং ক্ষুদ্রতম মানগুলি খুঁজে বের করার সময় এক্সট্রিম পয়েন্টটি ব্যবহার করা হয়, যেহেতু তারা ব্যবধান থেকে ফাংশন বাড়ায় বা হ্রাস করে।

এই নিবন্ধটি সংজ্ঞা প্রকাশ করে, আমরা ব্যবধানে বৃদ্ধি এবং হ্রাসের একটি পর্যাপ্ত চিহ্ন এবং একটি চরমের অস্তিত্বের শর্ত তৈরি করি। এটি উদাহরণ এবং সমস্যা সমাধানের ক্ষেত্রে প্রযোজ্য। ফাংশনের পার্থক্য সংক্রান্ত বিভাগটি পুনরাবৃত্তি করা উচিত, কারণ সমাধান করার সময় এটি ডেরিভেটিভ খুঁজে বের করা ব্যবহার করতে হবে।

Yandex.RTB R-A-339285-1 সংজ্ঞা 1

যে কোনো x 1 ∈ X এবং x 2 ∈ X , x 2 > x 1 এর জন্য অসমতা f (x 2) > f (x 1) সম্ভব হলে y = f (x) ব্যবধান x-এ বৃদ্ধি পাবে। অন্য কথায়, আর্গুমেন্টের একটি বৃহত্তর মান ফাংশনের একটি বৃহত্তর মানের সাথে মিলে যায়।

সংজ্ঞা 2

যে কোনো x 1 ∈ X , x 2 ∈ X , x 2 > x 1 এর জন্য সমতা f (x 2) > f (x 1) বিবেচিত হলে y = f (x) ফাংশনটি x ব্যবধানে হ্রাস পাচ্ছে বলে মনে করা হয় সম্ভাব্য. অন্য কথায়, একটি বড় ফাংশন মান একটি ছোট আর্গুমেন্ট মানের সাথে মিলে যায়। নীচের চিত্রটি বিবেচনা করুন।

মন্তব্য: যখন ফাংশনটি আরোহী এবং অবরোহ ব্যবধানের শেষে নির্দিষ্ট এবং অবিচ্ছিন্ন থাকে, অর্থাৎ (a; b) যেখানে x = a, x = b, পয়েন্টগুলি আরোহী এবং অবরোহ ব্যবধানে অন্তর্ভুক্ত হয়। এটি সংজ্ঞার বিরোধিতা করে না, যার মানে এটি x ব্যবধানে ঘটে।

y = sin x টাইপের প্রাথমিক ফাংশনের প্রধান বৈশিষ্ট্য হল আর্গুমেন্টের বাস্তব মানের জন্য নির্দিষ্টতা এবং ধারাবাহিকতা। এখান থেকে আমরা পাই যে সাইনের বৃদ্ধি ব্যবধানে ঘটে - π 2; π 2, তারপর সেগমেন্টে বৃদ্ধির ফর্ম আছে - π 2; π 2।

সংজ্ঞা 3

বিন্দু x 0 বলা হয় সর্বোচ্চ পয়েন্টএকটি ফাংশনের জন্য y = f (x) যখন x এর সমস্ত মানের জন্য অসমতা f (x 0) ≥ f (x) সত্য। সর্বাধিক ফাংশনবিন্দুতে ফাংশনের মান, এবং y m a x দ্বারা চিহ্নিত করা হয়।

x 0 বিন্দুটিকে y \u003d f (x) ফাংশনের সর্বনিম্ন বিন্দু বলা হয় যখন x এর সমস্ত মানের জন্য অসমতা f (x 0) ≤ f (x) সত্য হয়। ফিচার ন্যূনতমবিন্দুতে ফাংশনের মান এবং y m i n ফর্মের স্বরলিপি রয়েছে।

বিন্দু x 0 এর আশেপাশের এলাকা বিবেচনা করা হয় চরম বিন্দু,এবং ফাংশনের মান যা এক্সট্রিমাম পয়েন্টের সাথে মিলে যায়। নীচের চিত্রটি বিবেচনা করুন।

ফাংশনের সবচেয়ে বড় এবং ক্ষুদ্রতম মান সহ ফাংশনের এক্সট্রিমা। নীচের চিত্রটি বিবেচনা করুন।

প্রথম চিত্রে বলা হয়েছে যে সেগমেন্ট থেকে ফাংশনের সবচেয়ে বড় মান খুঁজে বের করা প্রয়োজন [ a ; খ] এটি সর্বাধিক বিন্দু ব্যবহার করে পাওয়া যায় এবং ফাংশনের সর্বোচ্চ মানের সমান, এবং দ্বিতীয় চিত্রটি x = b এ সর্বাধিক বিন্দু খুঁজে পাওয়ার মতো।

ফাংশন বৃদ্ধি এবং হ্রাস করার জন্য যথেষ্ট শর্ত

একটি ফাংশনের সর্বোচ্চ এবং মিনিমাম খুঁজে বের করার জন্য, যখন ফাংশনটি এই শর্তগুলিকে সন্তুষ্ট করে তখন একটি এক্সট্রিমামের চিহ্নগুলি প্রয়োগ করা প্রয়োজন৷ প্রথম বৈশিষ্ট্যটি সবচেয়ে বেশি ব্যবহৃত হয়।

একটি extremum জন্য প্রথম যথেষ্ট শর্ত

সংজ্ঞা 4

একটি ফাংশন y = f (x) দেওয়া যাক, যা x 0 বিন্দুর ε আশেপাশে পার্থক্যযোগ্য, এবং প্রদত্ত বিন্দু x 0 এ ধারাবাহিকতা রয়েছে। তাই আমরা যে পেতে

• যখন f "(x) > 0 এর সাথে x ∈ (x 0 - ε; x 0) এবং f" (x)< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• যখন f"(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >x ∈ (x 0; x 0 + ε) এর জন্য 0, তারপর x 0 হল সর্বনিম্ন বিন্দু।

অন্য কথায়, আমরা তাদের চিহ্ন নির্ধারণের শর্তগুলি পাই:

• যখন ফাংশনটি x 0 বিন্দুতে অবিচ্ছিন্ন থাকে, তখন এটিতে একটি পরিবর্তনশীল চিহ্ন সহ একটি ডেরিভেটিভ থাকে, অর্থাৎ + থেকে -, যার অর্থ বিন্দুটিকে সর্বাধিক বলা হয়;
• যখন ফাংশনটি x 0 বিন্দুতে অবিচ্ছিন্ন থাকে, তখন এটি থেকে - থেকে + পরিবর্তনশীল চিহ্ন সহ একটি ডেরিভেটিভ থাকে, যার অর্থ বিন্দুটিকে সর্বনিম্ন বলা হয়।

ফাংশনের সর্বোচ্চ এবং সর্বনিম্ন পয়েন্ট সঠিকভাবে নির্ধারণ করতে, আপনাকে সেগুলি খুঁজে বের করার জন্য অ্যালগরিদম অনুসরণ করতে হবে:

• সংজ্ঞার ডোমেন খুঁজুন;
• এই এলাকায় ফাংশনের ডেরিভেটিভ খুঁজুন;
• শূন্য এবং বিন্দু সনাক্ত করুন যেখানে ফাংশন বিদ্যমান নেই;
• ব্যবধানে ডেরিভেটিভের চিহ্ন নির্ধারণ করা;
• বিন্দু নির্বাচন করুন যেখানে ফাংশন পরিবর্তন চিহ্ন.

ফাংশনের চরমতা খুঁজে বের করার কয়েকটি উদাহরণ সমাধানের উদাহরণে অ্যালগরিদমটি বিবেচনা করুন।

উদাহরণ 1

প্রদত্ত ফাংশন y = 2 (x + 1) 2 x - 2 এর সর্বাধিক এবং সর্বনিম্ন বিন্দুগুলি খুঁজুন।

সমাধান

এই ফাংশনের ডোমেইন হল x = 2 ছাড়া সব বাস্তব সংখ্যা। প্রথমত, আমরা ফাংশনের ডেরিভেটিভ খুঁজে পাই এবং পাই:

y "= 2 x + 1 2 x - 2" = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2) " (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2) ) - (x + 2) 2 (x - 2) 2 = = 2 (x + 1) (x - 5) (x - 2) 2

এখান থেকে আমরা দেখতে পাচ্ছি যে ফাংশনের শূন্যগুলি হল x \u003d - 1, x \u003d 5, x \u003d 2, অর্থাৎ প্রতিটি বন্ধনীকে শূন্যের সমান করতে হবে। নম্বর লাইনে চিহ্নিত করুন এবং পান:

এখন আমরা প্রতিটি ব্যবধান থেকে ডেরিভেটিভের লক্ষণগুলি নির্ধারণ করি। ব্যবধানে অন্তর্ভুক্ত একটি বিন্দু নির্বাচন করা প্রয়োজন, এটিকে অভিব্যক্তিতে প্রতিস্থাপন করুন। উদাহরণস্বরূপ, পয়েন্ট x = - 2, x = 0, x = 3, x = 6।

আমরা যে পেতে

y "(- 2) \u003d 2 (x + 1) (x - 5) (x - 2) 2 x \u003d - 2 \u003d 2 (- 2 + 1) (- 2 - 5) (- 2 - 2 ) 2 \u003d 2 7 16 \u003d 7 8 > 0, তাই, ব্যবধান - ∞; - 1 এর একটি ধনাত্মক ডেরিভেটিভ আছে। একইভাবে, আমরা এটি পাই

y "(0) = 2 (0 + 1) 0 - 5 0 - 2 2 = 2 - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

যেহেতু দ্বিতীয় ব্যবধান পরিণত শূন্যের চেয়ে কম, তাই সেগমেন্টের ডেরিভেটিভ নেতিবাচক হবে। একটি বিয়োগ সঙ্গে তৃতীয়, একটি প্লাস সঙ্গে চতুর্থ. ধারাবাহিকতা নির্ধারণের জন্য, ডেরিভেটিভের চিহ্নের দিকে মনোযোগ দেওয়া প্রয়োজন, যদি এটি পরিবর্তিত হয় তবে এটি একটি চরম বিন্দু।

আমরা পাই যে x = - 1 বিন্দুতে ফাংশনটি অবিচ্ছিন্ন থাকবে, যার অর্থ হল ডেরিভেটিভ + থেকে - চিহ্ন পরিবর্তন করবে। প্রথম চিহ্ন অনুসারে, আমাদের আছে যে x = - 1 হল সর্বাধিক বিন্দু, যার মানে আমরা পাই

y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0

বিন্দু x = 5 নির্দেশ করে যে ফাংশনটি অবিচ্ছিন্ন, এবং ডেরিভেটিভটি - থেকে + চিহ্ন পরিবর্তন করবে। তাই, x=-1 হল সর্বনিম্ন বিন্দু, এবং এর ফাইন্ডিং এর ফর্ম আছে

y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24

গ্রাফিক ইমেজ

উত্তর: y m a x = y (- 1) = 0 , y m i n = y (5) = 24।

এটি এই বিষয়টিতে মনোযোগ দেওয়ার মতো যে একটি চরমের প্রথম পর্যাপ্ত চিহ্ন ব্যবহার করার জন্য ফাংশনটিকে বিন্দু x 0 থেকে আলাদা করার প্রয়োজন হয় না এবং এটি গণনাটিকে সহজ করে তোলে।

উদাহরণ 2

y = 1 6 x 3 = 2 x 2 + 22 3 x - 8 ফাংশনের সর্বাধিক এবং সর্বনিম্ন বিন্দুগুলি খুঁজুন।

সমাধান।

একটি ফাংশনের ডোমেইন হল সমস্ত বাস্তব সংখ্যা। এটি ফর্মের সমীকরণের একটি সিস্টেম হিসাবে লেখা যেতে পারে:

1 6 x 3 - 2 x 2 - 22 3 x - 8 , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

তারপরে আপনাকে ডেরিভেটিভ খুঁজে বের করতে হবে:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

বিন্দু x = 0 এর কোন ডেরিভেটিভ নেই, কারণ একতরফা সীমার মান ভিন্ন। আমরা এটি পাই:

lim y "x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 lim y "x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3

এটি অনুসরণ করে যে ফাংশনটি x = 0 বিন্দুতে অবিচ্ছিন্ন থাকে, তারপর আমরা গণনা করি

lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 (0 - 0) 3 - 2 (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 লিম y x → 0 + 0 = লিম x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 ( 0 + 0) 2 + 22 3 (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 0 3 - 2 0 2 + 22 3 0 - 8 = - 8

যখন ডেরিভেটিভ শূন্য হয়ে যায় তখন আর্গুমেন্টের মান খুঁজে বের করার জন্য গণনা করা প্রয়োজন:

1 2 x 2 - 4 x - 22 3 , x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0

প্রতিটি ব্যবধানের চিহ্ন নির্ধারণ করতে প্রাপ্ত সমস্ত পয়েন্ট অবশ্যই লাইনে চিহ্নিত করতে হবে। অতএব, প্রতিটি ব্যবধানের জন্য নির্বিচারে বিন্দুতে ডেরিভেটিভ গণনা করা প্রয়োজন। উদাহরণস্বরূপ, আমরা x = - 6 , x = - 4 , x = - 1 , x = 1 , x = 4 , x = 6 মান সহ পয়েন্ট নিতে পারি। আমরা যে পেতে

y " (- 6) \u003d - 1 2 x 2 - 4 x - 22 3 x \u003d - 6 \u003d - 1 2 - 6 2 - 4 (- 6) - 22 3 \u003d - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y "(- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 (- 1) 2 - 4 (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

একটি সরল রেখার চিত্রের ফর্ম আছে

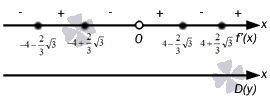
সুতরাং, আমরা এই বিন্দুতে আসি যে চরমের প্রথম চিহ্নটি অবলম্বন করা প্রয়োজন। আমরা গণনা করে তা পাই

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , তারপর এখান থেকে সর্বোচ্চ পয়েন্টের মান x = - 4 + 2 3 3 , x = 4 - 2 3 3

আসুন ন্যূনতম গণনা করা যাক:

y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

আসুন আমরা ফাংশনের সর্বোচ্চ হিসাব করি। আমরা যে পেতে

y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

গ্রাফিক ইমেজ

উত্তর:

y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 y 27 x 3 = y 4 - 2 3 3 = 8 27 3

যদি ফাংশন f "(x 0) = 0 দেওয়া হয়, তাহলে এর f "" (x 0) > 0 দিয়ে আমরা পাই যে x 0 হল সর্বনিম্ন বিন্দু যদি f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

উদাহরণ 3

y = 8 x x + 1 ফাংশনের সর্বোচ্চ এবং মিনিমাম নির্ণয় কর।

সমাধান

প্রথমত, আমরা সংজ্ঞার ডোমেন খুঁজে পাই। আমরা যে পেতে

D (y) : x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

ফাংশনটি আলাদা করা প্রয়োজন, যার পরে আমরা পাই

y "= 8 x x + 1" = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x

যখন x = 1, ডেরিভেটিভটি শূন্যের সমান হয়ে যায়, যার মানে হল বিন্দুটি একটি সম্ভাব্য প্রান্ত। স্পষ্টীকরণের জন্য, দ্বিতীয় ডেরিভেটিভ খুঁজে বের করতে হবে এবং x \u003d 1-এ মান গণনা করতে হবে। আমরা পেতে:

y "" = 4 - x + 1 (x + 1) 2 x " = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x "(x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2" x + (x + 1) 2 x "(x + 1) 4 x == 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1)" x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1 ) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 - 4 8 = - 1< 0

তাই, এক্সট্রিমামের জন্য 2টি যথেষ্ট শর্ত ব্যবহার করে, আমরা পাই যে x = 1 হল সর্বাধিক বিন্দু। অন্যথায়, এন্ট্রিটি y m a x = y (1) = 8 1 1 + 1 = 4।

গ্রাফিক ইমেজ

উত্তর: y m a x = y (1) = 4 ..

সংজ্ঞা 5

y = f (x) ফাংশনটির প্রদত্ত বিন্দু x 0 এর ε পার্শ্ববর্তী স্থানে nম ক্রম পর্যন্ত এর ডেরিভেটিভ রয়েছে এবং x 0 বিন্দুতে n + 1ম ক্রম পর্যন্ত এর ডেরিভেটিভ রয়েছে। তারপর f "(x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0।

এটি অনুসরণ করে যে যখন n একটি জোড় সংখ্যা হয়, তখন x 0 একটি প্রবর্তন বিন্দু হিসাবে বিবেচিত হয়, যখন n একটি বিজোড় সংখ্যা হয়, তখন x 0 একটি চরম বিন্দু এবং f (n + 1) (x 0) > 0, তারপর x 0 হল একটি সর্বনিম্ন বিন্দু, f(n+1)(x0)< 0 , тогда x 0 является точкой максимума.

উদাহরণ 4

y y = 1 16 (x + 1) 3 (x - 3) 4 ফাংশনের সর্বাধিক এবং সর্বনিম্ন বিন্দুগুলি খুঁজুন।

সমাধান

মূল ফাংশনটি একটি সম্পূর্ণ যুক্তিসঙ্গত, তাই এটি অনুসরণ করে যে সংজ্ঞার ডোমেন হল সমস্ত বাস্তব সংখ্যা। ফাংশন পার্থক্য করা প্রয়োজন. আমরা যে পেতে

y "= 1 16 x + 1 3" (x - 3) 4 + (x + 1) 3 x - 3 4 " == 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

এই ডেরিভেটিভ x 1 = - 1, x 2 = 5 7, x 3 = 3 এ শূন্যে যাবে। যে, পয়েন্ট একটি সম্ভাব্য চরম বিন্দু হতে পারে. তৃতীয় পর্যাপ্ত চরম অবস্থা প্রয়োগ করা প্রয়োজন। দ্বিতীয় ডেরিভেটিভ খুঁজে বের করা আপনাকে একটি ফাংশনের সর্বাধিক এবং সর্বনিম্ন উপস্থিতি সঠিকভাবে নির্ধারণ করতে দেয়। দ্বিতীয় ডেরিভেটিভ এর সম্ভাব্য প্রান্তের বিন্দুতে গণনা করা হয়। আমরা যে পেতে

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

এর মানে হল x 2 \u003d 5 7 হল সর্বাধিক বিন্দু। 3টি পর্যাপ্ত মানদণ্ড প্রয়োগ করে, আমরা n = 1 এবং f (n + 1) 5 7 এর জন্য পাই< 0 .

x 1 = - 1, x 3 = 3 বিন্দুর প্রকৃতি নির্ধারণ করা প্রয়োজন। এটি করার জন্য, আপনাকে তৃতীয় ডেরিভেটিভ খুঁজে বের করতে হবে, এই পয়েন্টগুলিতে মানগুলি গণনা করতে হবে। আমরা যে পেতে

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " == 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

সুতরাং, x 1 = - 1 হল ফাংশনের প্রবর্তন বিন্দু, যেহেতু n = 2 এবং f (n + 1) (- 1) ≠ 0 এর জন্য। বিন্দু x 3 = 3 তদন্ত করা প্রয়োজন। এটি করার জন্য, আমরা 4 র্থ ডেরিভেটিভ খুঁজে পাই এবং এই সময়ে গণনা সম্পাদন করি:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " == 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0

উপরের থেকে, আমরা উপসংহারে পৌঁছেছি যে x 3 \u003d 3 হল ফাংশনের সর্বনিম্ন বিন্দু।

গ্রাফিক ইমেজ

উত্তর: x 2 \u003d 5 7 হল সর্বাধিক বিন্দু, x 3 \u003d 3 - প্রদত্ত ফাংশনের সর্বনিম্ন বিন্দু।

আপনি যদি পাঠ্যটিতে একটি ভুল লক্ষ্য করেন, দয়া করে এটি হাইলাইট করুন এবং Ctrl+Enter টিপুন

"ফাংশন বৃদ্ধি এবং হ্রাস"

পাঠের উদ্দেশ্য:

1. একঘেয়েতার ব্যবধান খুঁজে পেতে শিখুন।

2. মানসিক ক্ষমতার বিকাশ যা পরিস্থিতির বিশ্লেষণ এবং কর্মের পর্যাপ্ত পদ্ধতির বিকাশ প্রদান করে (বিশ্লেষণ, সংশ্লেষণ, তুলনা)।

3. বিষয়ের প্রতি আগ্রহের গঠন।

ক্লাস চলাকালীন

আজ আমরা ডেরিভেটিভের প্রয়োগ অধ্যয়ন চালিয়ে যাচ্ছি এবং ফাংশন অধ্যয়নের জন্য এর প্রয়োগের প্রশ্নটি বিবেচনা করছি। সামনে কাজ

এবং এখন "Brainstorm" ফাংশনের বৈশিষ্ট্যগুলির কিছু সংজ্ঞা দেওয়া যাক

1. ফাংশন কাকে বলে?

2. x চলকের নাম কি?

3. Y চলকের নাম কি?

4. একটি ফাংশনের সুযোগ কি?

5. একটি ফাংশন মান সেট কি?

6. একটি জোড় ফাংশন কি?

7. কোন ফাংশনকে বিজোড় বলা হয়?

8. একটি জোড় ফাংশনের গ্রাফ সম্পর্কে কী বলা যেতে পারে?

9. একটি বিজোড় ফাংশনের গ্রাফ সম্পর্কে কি বলা যেতে পারে?

10. একটি ক্রমবর্ধমান ফাংশন কি?

11. একটি হ্রাস ফাংশন কি?

12. একটি পর্যায়ক্রমিক ফাংশন কি?

গণিত গাণিতিক মডেল অধ্যয়ন করে। সবচেয়ে গুরুত্বপূর্ণ এক গাণিতিক মডেলএকটি ফাংশন। বিদ্যমান ভিন্ন পথফাংশন বর্ণনা। কোনটি সবচেয়ে সুস্পষ্ট?

- গ্রাফিক।

- কিভাবে একটি গ্রাফ তৈরি করতে হয়?

- পয়েন্ট দ্বারা।

এই পদ্ধতিটি উপযুক্ত যদি আপনি আগে থেকেই জানেন যে গ্রাফটি কেমন দেখাচ্ছে। উদাহরণস্বরূপ, একটি দ্বিঘাত ফাংশনের গ্রাফ, একটি রৈখিক ফাংশন, একটি বিপরীত সমানুপাতিকতা, একটি ফাংশন y = sinx কী? (সংশ্লিষ্ট সূত্রগুলি প্রদর্শিত হয়, শিক্ষার্থীরা রেখাচিত্রগুলির নাম দেয়।)

কিন্তু যদি আপনি একটি ফাংশন বা আরও জটিল এক গ্রাফ করতে চান? আপনি একাধিক পয়েন্ট খুঁজে পেতে পারেন, কিন্তু কিভাবে ফাংশন এই পয়েন্টগুলির মধ্যে আচরণ করে?

বোর্ডে দুটি পয়েন্ট রাখুন, শিক্ষার্থীদের "তাদের মধ্যে" গ্রাফটি দেখতে কেমন হতে পারে তা দেখাতে বলুন:

একটি ফাংশন কিভাবে আচরণ করে তা খুঁজে বের করতে, এর ডেরিভেটিভ সাহায্য করে।

নোটবুক খুলুন, নম্বর লিখুন, ক্লাসের কাজ করুন।

পাঠের উদ্দেশ্য: কীভাবে একটি ফাংশনের গ্রাফ তার ডেরিভেটিভের গ্রাফের সাথে সম্পর্কিত তা শিখুন এবং কীভাবে দুটি ধরণের সমস্যা সমাধান করবেন তা শিখুন:

1. ডেরিভেটিভের গ্রাফ অনুসারে, ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধানগুলি, সেইসাথে ফাংশনের চরম বিন্দুগুলি সন্ধান করুন;

2. ব্যবধানে ডেরিভেটিভের লক্ষণগুলির স্কিম অনুসারে, ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধানগুলি, সেইসাথে ফাংশনের চরম বিন্দুগুলি সন্ধান করুন।

এই জাতীয় কাজগুলি আমাদের পাঠ্যপুস্তকে নেই, তবে এগুলি ইউনিফাইড স্টেট পরীক্ষার (অংশ A এবং B) পরীক্ষায় পাওয়া যায়।

আজ পাঠে আমরা প্রক্রিয়াটি অধ্যয়নের দ্বিতীয় পর্যায়ের কাজের একটি ছোট উপাদান বিবেচনা করব, ফাংশনের একটি বৈশিষ্ট্যের অধ্যয়ন - একঘেয়েমি ব্যবধানের সংজ্ঞা।

এই সমস্যা সমাধানের জন্য, আমাদের আগে আলোচিত কিছু বিষয় স্মরণ করতে হবে।

সুতরাং, আসুন আজকের পাঠের বিষয়টি লিখি: ফাংশন বৃদ্ধি এবং হ্রাসের লক্ষণ।

কার্যকারিতা বৃদ্ধি এবং হ্রাসের লক্ষণ:

যদি এই ফাংশনের ডেরিভেটিভটি ব্যবধানে (a; c), অর্থাৎ f "(x)\u003e 0-এ x এর সমস্ত মানের জন্য ধনাত্মক হয়, তবে এই ব্যবধানে ফাংশনটি বৃদ্ধি পায়।
যদি এই ফাংশনের ডেরিভেটিভটি ব্যবধানে (a; b) x এর সমস্ত মানের জন্য ঋণাত্মক হয়, যেমন f "(x)< 0, то функция в этом интервале убывает

একঘেয়েতার ব্যবধান খোঁজার ক্রম:

ফাংশনের সুযোগ সন্ধান করুন।

1. একটি ফাংশনের প্রথম ডেরিভেটিভ খুঁজুন।

2. বোর্ডে সিদ্ধান্ত নিন

সমালোচনামূলক পয়েন্ট খুঁজুন, ব্যবধানে প্রথম ডেরিভেটিভের চিহ্ন অনুসন্ধান করুন যেখানে পাওয়া সমালোচনামূলক পয়েন্টগুলি ফাংশনের ডোমেনকে বিভক্ত করে। ফাংশনের একঘেয়েতার ব্যবধান খুঁজুন:

ক) সংজ্ঞার ক্ষেত্র,

খ) প্রথম ডেরিভেটিভ খুঁজুন:,

গ) গুরুত্বপূর্ণ পয়েন্ট খুঁজুন: ; , এবং

3. আমরা প্রাপ্ত বিরতিতে ডেরিভেটিভের চিহ্নটি তদন্ত করি, সমাধানটি একটি টেবিলের আকারে উপস্থাপন করা হয়।

চরম পয়েন্টের দিকে নির্দেশ করুন

আসুন বৃদ্ধি এবং হ্রাসের জন্য একটি ফাংশন পরীক্ষা করার কয়েকটি উদাহরণ দেখি।

সর্বাধিক অস্তিত্বের জন্য একটি পর্যাপ্ত শর্ত হল "+" থেকে "-" তে ক্রিটিক্যাল পয়েন্টের মধ্য দিয়ে যাওয়ার সময় ডেরিভেটিভের চিহ্ন পরিবর্তন করা এবং সর্বনিম্ন জন্য "-" থেকে "+"। যদি ক্রিটিক্যাল পয়েন্টের মধ্য দিয়ে যাওয়ার সময় ডেরিভেটিভটি চিহ্ন পরিবর্তন না করে, তাহলে এই বিন্দুতে কোন এক্সট্রিম নেই

1. D(f) খুঁজুন।

2. f "(x) খুঁজুন।

3. স্থির বিন্দু খুঁজুন, যেমন বিন্দু যেখানে f"(x) = 0 বা f"(x) বিদ্যমান নেই।
(লবের শূন্যে ডেরিভেটিভটি 0, হরটির শূন্যে ডেরিভেটিভের অস্তিত্ব নেই)

4. স্থানাঙ্ক লাইনে D(f) এবং এই বিন্দুগুলি সনাক্ত করুন।

5. প্রতিটি ব্যবধানে ডেরিভেটিভের চিহ্নগুলি নির্ধারণ করুন

6. চিহ্ন প্রয়োগ করুন।

7. উত্তর লিখুন।

নতুন উপাদান একীকরণ.

শিক্ষার্থীরা জোড়ায় জোড়ায় কাজ করে এবং তাদের নোটবুকে তাদের সমাধান লেখে।

ক) y \u003d x³ - 6 x² + 9 x - 9;

b) y \u003d 3 x² - 5x + 4।

ব্ল্যাকবোর্ডে দুইজন কাজ করে।

ক) y \u003d 2 x³ - 3 x² - 36 x + 40

খ) y \u003d x4-2 x³

3.পাঠের সারাংশ

বাড়ির কাজ: পরীক্ষা (পার্থক্য)

একঘেয়ে

উচ্চ গুরুত্বপূর্ণ সম্পত্তিফাংশন তার একঘেয়েমি। বিভিন্ন বিশেষ ক্রিয়াকলাপের এই বৈশিষ্ট্যটি জেনে, আপনি বিভিন্ন শারীরিক, অর্থনৈতিক, সামাজিক এবং অন্যান্য অনেক প্রক্রিয়ার আচরণ নির্ধারণ করতে পারেন।

নিম্নলিখিত ধরনের ফাংশন একঘেয়েমি আলাদা করা হয়:

1) ফাংশন বৃদ্ধি পায়, যদি কিছু ব্যবধানে, যদি কোন দুটি পয়েন্টের জন্য এবং এই ব্যবধানটি যেমন। সেগুলো. আর্গুমেন্টের একটি বড় মান ফাংশনের একটি বৃহত্তর মানের সাথে মিলে যায়;

2) ফাংশন হ্রাস, যদি কিছু ব্যবধানে, যদি কোন দুটি পয়েন্টের জন্য এবং এই ব্যবধানটি যেমন। সেগুলো. আর্গুমেন্টের একটি বড় মান ফাংশনের একটি ছোট মানের সাথে মিলে যায়;

3) ফাংশন অ-হ্রাস, যদি কিছু ব্যবধানে, যদি কোন দুটি পয়েন্টের জন্য এবং এই ব্যবধানটি যেমন;

4) ফাংশন বাড়ে না, যদি কিছু ব্যবধানে, যদি কোন দুটি পয়েন্টের জন্য এবং এই ব্যবধানটি যেমন।

2. প্রথম দুটি ক্ষেত্রে, "কঠোর একঘেয়েমি" শব্দটিও ব্যবহৃত হয়।

3. শেষ দুটি ক্ষেত্রে নির্দিষ্ট এবং সাধারণত বিভিন্ন ফাংশনের একটি রচনা হিসাবে নির্দিষ্ট করা হয়।

4. আলাদাভাবে, আমরা লক্ষ্য করি যে ফাংশনের গ্রাফের বৃদ্ধি এবং হ্রাস বাম থেকে ডানে ঠিক বিবেচনা করা উচিত এবং অন্য কিছু নয়।

2. জোড়/বিজোড়।

ফাংশনটিকে বিজোড় বলা হয়, যদি আর্গুমেন্টের চিহ্ন পরিবর্তিত হয়, এটি তার মানকে বিপরীতে পরিবর্তন করে। এই জন্য সূত্র এই মত দেখায় . এর মানে হল সব x এর জায়গায় বিয়োগ x মানগুলিকে ফাংশনে প্রতিস্থাপন করার পরে, ফাংশনটি তার চিহ্ন পরিবর্তন করবে। এই ধরনের ফাংশনের গ্রাফ উৎপত্তি সম্পর্কে প্রতিসম।

বিজোড় ফাংশনের উদাহরণ ইত্যাদি।

উদাহরণস্বরূপ, গ্রাফটি প্রকৃতপক্ষে উত্স সম্পর্কে প্রতিসম:

ফাংশন বলা হয় এমনকিযদি যুক্তির চিহ্ন পরিবর্তন করলে তার মান পরিবর্তন হয় না। এই জন্য সূত্র এই মত দেখায়. এর মানে হল যে সমস্ত x এর জায়গায় বিয়োগ x মানগুলিকে ফাংশনে প্রতিস্থাপন করার পরে, ফলস্বরূপ ফাংশনটি পরিবর্তন হবে না। এই ধরনের ফাংশনের গ্রাফটি অক্ষ সম্পর্কে প্রতিসম।

জোড় ফাংশনের উদাহরণ ইত্যাদি।

উদাহরণস্বরূপ, আসুন অক্ষ সম্পর্কে গ্রাফের প্রতিসাম্য দেখাই:

যদি একটি ফাংশন নির্দিষ্ট ধরনের কোনটির অন্তর্গত না হয়, তাহলে তাকে বলা হয় জোড় বা বিজোড় নয়, বা ফাংশন সাধারণ দৃষ্টিকোণ . এই ধরনের ফাংশনগুলির প্রতিসাম্য নেই।

যেমন একটি ফাংশন, উদাহরণস্বরূপ, একটি গ্রাফ সহ সম্প্রতি বিবেচিত লিনিয়ার ফাংশন:

3. ফাংশনের একটি বিশেষ বৈশিষ্ট্য হল পর্যায়ক্রমিকতা

আসল বিষয়টি হল যে পর্যায়ক্রমিক ফাংশনগুলি যা মানক স্কুল পাঠ্যক্রমে বিবেচনা করা হয় তা শুধুমাত্র ত্রিকোণমিতিক ফাংশন। সংশ্লিষ্ট বিষয় অধ্যয়ন করার সময় আমরা ইতিমধ্যে তাদের সম্পর্কে বিস্তারিতভাবে কথা বলেছি।

পর্যায়ক্রমিক ফাংশনএকটি ফাংশন যা আর্গুমেন্টে একটি নির্দিষ্ট ধ্রুবক নন-জিরো সংখ্যা যোগ করা হলে এর মান পরিবর্তন করে না।

এই সর্বনিম্ন সংখ্যা বলা হয় ফাংশন সময়কালএবং একটি অক্ষর দ্বারা চিহ্নিত করা হয়.

এই জন্য সূত্র এই মত দেখায়:

আসুন সাইন গ্রাফের উদাহরণে এই সম্পত্তিটি দেখি:

স্মরণ করুন যে ফাংশনের সময়কাল এবং হল , এবং এবং এর সময়কাল।

আমরা ইতিমধ্যে জানি, একটি জটিল যুক্তি সহ ত্রিকোণমিতিক ফাংশনের জন্য একটি অ-মানক সময় থাকতে পারে। এই ফর্মের ফাংশন:

তাদের একই সময়কাল আছে। এবং ফাংশন সম্পর্কে:

তাদের একই সময়কাল আছে।

আপনি দেখতে পাচ্ছেন, একটি নতুন পিরিয়ড গণনা করার জন্য, স্ট্যান্ডার্ড পিরিয়ডকে কেবল যুক্তিতে ফ্যাক্টর দ্বারা ভাগ করা হয়। এটি ফাংশনের অন্যান্য পরিবর্তনের উপর নির্ভর করে না।

সীমাবদ্ধতা।

ফাংশন y=f(x) X⊂D(f) সেটের নিচে থেকে আবদ্ধ বলা হয় যদি এমন একটি সংখ্যা থাকে যা কোনো xϵX-এর জন্য অসমতা f(x)< a.

ফাংশন y=f(x) X⊂D(f) সেটের উপরে থেকে আবদ্ধ বলা হয় যদি এমন একটি সংখ্যা থাকে যা কোনো xϵX-এর জন্য অসমতা f(x)< a.

যদি ব্যবধান X নির্দেশিত না হয়, তাহলে এটি বিবেচনা করা হয় যে ফাংশনটি সংজ্ঞার সম্পূর্ণ ডোমেনে সীমাবদ্ধ। একটি ফাংশন উপরে এবং নীচে উভয় সীমাবদ্ধ বলা হয়.

ফাংশনের সীমাবদ্ধতা গ্রাফ থেকে পড়া সহজ। কিছু সরল রেখা y=a আঁকা সম্ভব, এবং যদি ফাংশনটি এই সরলরেখার চেয়ে বেশি হয়, তাহলে এটি নীচে থেকে আবদ্ধ।

যদি নীচে, তারপর যথাক্রমে উপরে। নীচে একটি নিম্ন আবদ্ধ ফাংশন একটি গ্রাফ আছে. একটি আবদ্ধ ফাংশনের গ্রাফ, বন্ধুরা, এটি নিজে আঁকার চেষ্টা করুন।

বিষয়: ফাংশনের বৈশিষ্ট্য: বৃদ্ধি এবং হ্রাসের ব্যবধান; সর্বশ্রেষ্ঠ এবং ক্ষুদ্রতম মান; চরম বিন্দু (স্থানীয় সর্বোচ্চ এবং সর্বনিম্ন), ফাংশন উত্তলতা।

বৃদ্ধি এবং হ্রাসের সময়কাল।

ফাংশনের বৃদ্ধি এবং হ্রাসের জন্য পর্যাপ্ত অবস্থার (লক্ষণ) ভিত্তিতে, ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধান পাওয়া যায়।

ব্যবধানে ফাংশন বৃদ্ধি এবং হ্রাসের লক্ষণগুলির সূত্রগুলি এখানে রয়েছে:

যদি ফাংশনের ডেরিভেটিভ হয় y=f(x)যে কোনো জন্য ইতিবাচক এক্সব্যবধান থেকে এক্স, তারপর ফাংশন বৃদ্ধি পায় এক্স;

যদি ফাংশনের ডেরিভেটিভ হয় y=f(x)যে কোনো জন্য নেতিবাচক এক্সব্যবধান থেকে এক্স, তারপর ফাংশন কমে যায় এক্স.

সুতরাং, একটি ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধান নির্ধারণ করতে, এটি প্রয়োজনীয়:

ফাংশনের সুযোগ সন্ধান করুন;

একটি ফাংশনের ডেরিভেটিভ খুঁজুন;

বৈষম্য সমাধান এবং সংজ্ঞার ডোমেনে;